Approximations

We started learning the stuff on 4.7 in the book, which was about approximations. We learned how to approximate using the tangent lines and Newton's method. Curves are difficult to approximate so we use derivatives.

The class however started with us solving these root questions:

square root of 9
square root of 8
square root of 36
square root of 37

The only ones important were square root of 8 and square root of 37 because they aren't perfect squares and we can't approximate it exactly.

This is the root x function, which is the positive half of a sideways parabola.

To approximate root of 8 we use the closest perfect square to it, which is the coordinates (9,3). From that point we can make a tangent line. The purpose of the tangent line is to approximate the the point where x=8 on the curve. However, we only know the tangent line touches the point (9,3), which is on both the curve and the tangent. From this we can make the equation of the tangent line using the formula:

y-y₁=m(x-x₁).

First we need the slope at the point (9,3). So we find the derivative of the curve at that point which is it's slope. Using the power rule we find the derivative is (1/2)x^(-1/2) . After plugging in 9 in x we get the slope at that point is 1/6. Now we have all the variables needed to make the equation.

y-3=(1/6)(x-9)

f(x)=(1/6)x+(3/2)

Now that we have the equation of the tangent line we can use it to approximate the value when x=8 because the tangent line touches near it. After plugging in 8 in the function above we get the number 17/6. To see how close our approximation was we find the difference between the 2 values. (17/6)-square root of 8 = 0.0049. This is called the error.

It is the same process to find the value of square root of 37. We found out though that the error is much smaller. It's because the derivative of the tangent is decreasing as the x values increase. The derivative of the tangent is called the 2nd derivative, which is pretty much the slope of the slope.

Some other facts:

-The approximation will never be below the real value

-because graph is concave down

-the tangent line will always be above the curve

Newton's Method

I've been dreading explaining the beast that is called Newton's Method all day. As Mr. K says there's a difference between long and hard? Well I'm not going to quote him on that but he says something along those lines. I'll just do a little intro to it and leave the rest for the scribe tomorrow to carry on XD.

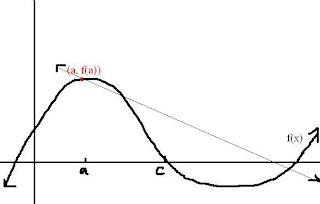
ANYWAYS, suppose we have a function that looks like the one below and we want to find its root.

First we make an estimate at a point near the root like at (a, f(a)). Just like how we solved square root of 8 with tangent approximations, we use that process here. Imagine that as a tangent line not a secant line =( .

y-f(a)=f prime (a)(x-a)
(plugging in the points in the point slope formula)

0-f(a)=f prime(a)(x-a)

(since we're looking for a root, y=0)

(-f(a)/f prime (a))+ a = x

We can see that our approximation is no where near the root of the function. So we have to make another tangent line on the function where there was a root on the tangent line. You repeat this process until you eventually get closer to the root.

I know my explanation of Newton's method sucked but i tried :(. Doing my scribe just made me realize how much i miss our smartboard

Next scribe is Kristina.