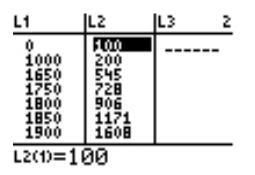
Anywho, we mostly worked with the formula of a derivative (slope of a tangent line). If you've forgotten what that formula was, here it is again:

She also bestowed us the gift of notes as to what the derivative of a function is in more detail. Due to her not being able to post the slides with these notes on it till Thursday, I shall kindly post them here for anyone that missed it or was not quick enough to take them down.
"The derivative of a fcn (a gift she bestowed upon us, it is short for function) at a chosen input value describes the best linear approximation of the fcn near the x-value under consideration."
 With the help of this graph (I forgot the arrows at the ends of the parabola xD), we can see that in this case "a" is the inputted value mentioned in the above note and the ..faded...red line is the linear approximation of the fcn near that inputted value, "a".
With the help of this graph (I forgot the arrows at the ends of the parabola xD), we can see that in this case "a" is the inputted value mentioned in the above note and the ..faded...red line is the linear approximation of the fcn near that inputted value, "a"."For a fcn with a single real variable, the derivative at that point equals the slope of the tangent line of the graph."
Meaning that we can input that value into the derivative formula since the definition of a derivative is that it is the slope of a tangent line.
Wahoo, now for some examples she gave us!
In the first example, she gave us the function f(x) = 2x2 - 5x + 6. We were told to find f'(4). Solving this is as easy as bringing paper plates and cups for Pi Day (Yes, I'm thinking about it already). Back on track, all you have to do is input the value 4 into the derivative formula shown at the top of this post. If you're still lost, here is what it should look like as you work through the problem:
 Tada! The derivative is 11 since as "h" approaches 0, it is shown that the value is close to 11 thus the answer. Simple algebra, right?! And since some people may make mistakes in their algebra during a question like this, here's a song to help you (I was bored so I decided to search "math" on imeem TEEHEE)
Tada! The derivative is 11 since as "h" approaches 0, it is shown that the value is close to 11 thus the answer. Simple algebra, right?! And since some people may make mistakes in their algebra during a question like this, here's a song to help you (I was bored so I decided to search "math" on imeem TEEHEE)Kay, so it doesn't exactly help with the algebra...sorta, but I thought it was kinda neat so HA!
Back on track! The second example we got asked us to find the derivative of f(x) = x2 - 3x for a number "a". How we solve this is the exact same as the last example, except we are working with a variable, "a". Once solved, we should find out that the answer is:
 Now, if we were given a question where it asks us to find the derivative f'(1) for the same function given in the last example, you can do it the long and tedious way (but not hard!) by using the same procedure as example 1, but you don't have to! This is because we've already found the derivative for f(x) = x2 - 3x earlier, which is 2a - 3. We can simply think of that as a function and then input 1 into that and voila! Simple and easy, also elegant.
Now, if we were given a question where it asks us to find the derivative f'(1) for the same function given in the last example, you can do it the long and tedious way (but not hard!) by using the same procedure as example 1, but you don't have to! This is because we've already found the derivative for f(x) = x2 - 3x earlier, which is 2a - 3. We can simply think of that as a function and then input 1 into that and voila! Simple and easy, also elegant.For our last example, we were given the function f(x) = x2 and were asked to estimate the derivative at the points {-2, -1, 0, 1, 2}. First we must graph this. After you have graphed it, draw the tangent line to those points and then just take an estimate at what the slope of that tangent line is. To check your answer, just input the points into the derivative equation and that's that!
Now that that's out of the way, the next scribe is.. Not Paul. Thanks for the confusing name, Paul :(. Oh and starting from page 100 up to 105 is review on some of the stuff I've talked about. Also, homework is on page 105. There are 8 questions but just do enough of them till you understand it. Anyways, I'm done for tonight. Have a nice day :)