Friday, March 27, 2009
Thursday, March 26, 2009
Finishing off Euler's Method
First, we went over the homework that was assigned last night. My images may not show up because blogger is undergoing maintenance today according to the notices, shown here. So I will do my best with my scribe. I will fix it once blogger is back up and running.
Here was the homework that was supposed to be finished:

and

Mr.K put some of the values near the end. So if you are not getting those numbers, you are doing something incorrectly. One reason why may be because of rounding. Rounding is not recommended because it will cause inaccuracies. You may round on your paper, but store the values onto the calculator.
Okay after that, Mr.K introduced us to a new calculator program that does the Euler Method, similar to what we did yesterday, but faster and more accurately. The program also graphs the numerical results. So we looked at the differential function on the homework last night. We saw how we could improve the accuracy of Euler's Method. By making the changes in x smaller and increaing the number of times the method is applied will increase the accuracy of the curve that is formed to the actual graph.
After playing around with the Euler Program. We worked on more differential equation problems. Here is the first one:

The key to these types of questions is to write down what you know. What is given may be explicitly shown while some may require some thinking. For example, in the question above, we are told that the automobile starts from rest. That means that the automobile has zero velocity and has travel zero feet at time zero. We were also told that the acceleration is constant. An initial value is also given. Now that we know this we can solve the problem using anti-differentiation techniques.
Here is the second question:

The goal of this question was to find the year that the country ran out of gas. So to do this, lets see what we were given. First, we were given the amount of gas the country had. We were also given the rate of gas consumption function. Notice that we were give the rate of gas consumption. That means at t=0, no gas was consumed so that means A(0)=0. So to put the goal in algebraic terms we need to find t when A(t)=100. So we anti-differentiate the given function and find c. once that is done, just make that function equal to 100 and solve for t.
I noticed that Mr.K solved the problem using a function similar to an accumulation function. But if you actually evaluate the integral you will get the exact same function to equate to 100.
"There are more ways to skin a cat. But don't really skin a cat, because that is cruel!"
~Mr.K
Just a note and a heads up, Chapter 9.1 was nothing more than applying new terminology to old things. Chapter 9.2, which involved the slope fields, shows how to solve differential equations graphically (using a graph).Chapter 9.3 talks about differential equations numerically, creating a table of values. As predicted, Chapter 9.4 will involve solving differential equations symbolically, using only algebra. (YESSS!!)
That's all we did today. So homework is Chapter 9.3 all questions. The next scribe will be Justus.
Now to continue the Youtube tradition:
Here's a little game my brother told me about. It is so funny, I couldn't stop laughing when I started playing :P

Wednesday, March 25, 2009
It's all about Euler.

Euler also worked with many brilliant people, one such person is Goldbach, who stated that any even number larger than 2 can be written with the sum of any 2 prime numbers, if you feel like being famous some day, find an exception to this statement. Euler was also a father and he claimed to have made many mathematical discoveries while holding a baby in his hands, and as his other children played around his feet, now that is some fatherly love. Mr. K thought this was quite the favorable trait.
Now that we know a bit about Euler we can move on to his method. Which was the main focus in today's class. If we have a derivative that tells the slope of any line and you want to find a specific function, and not just a family of functions. You would need a slope and point, then you can get the equation of the line from the slope field. Calculate the equation of the line by moving a known point on one of the slope field lines by 0.1 units, find the slope at that point of the line then move the point 0.1 units on the new line and find a slope line at that new point, and repeat. Using the tangent lines gives a close approximation of the equation of the line. A great example is found on slide 2.

You can decrease the amount of error by using smaller intervals, such as 0.001 units instead of 0.01, but this is a very tedious process when done by hand. This method generates a table of values.
Another example we used was using local linear approximation to find 1.001100.

Find the derivative of the function by replacing 1.001 with x to make it easier. Then replace x with a number close to 1.001 such as 1, this will be the x-value. By solving the original equation the y-value given would be 1. Solving the derivative equation would give the slope, which is 100. Inputting this into the equation of a line and then replacing 1 with 1.001 to find a close approximation of the original value of 1.001100 which would be 1.1
Our homework is found on slides 6. We are given the initial point, the differential equation, the amount of steps between the given interval and the change in the x-value. The first few steps are done for us. All the equations we need to use are given at the top, and we find the slope by inputting the points in the differential equation. The change of x remains constant. Have fun.

and slide 7 is also homework.
 Also, great job to Jamie for her performance in the talent show! Good luck on your homework and the next scribe will be Benofschool.
Also, great job to Jamie for her performance in the talent show! Good luck on your homework and the next scribe will be Benofschool.
Tuesday, March 24, 2009
"Where My Little Bird Gets Caught In The Wind." - D. Kuropatwa.
I'm running out of creative titles, and my head is going in circles... BUT... let's get straight to it. I didn't scribe the other day, since we didn't have class. It's only fair, right?
As usual, we started off AP class breaking the ice...well that's not quite the ... correct term. We had a little chit chat session and in the middle of that, I told Mr. K, and judging by my natural loudness the whole class about my feelings about where my presence will be during Thursday's class. I was asking for his opinion, and I gave him the power of deciding for me, but we moved on to the lesson. Or... just another current topic in calculus.
Another PRE PRE LESSON... I am not making sense tonight. :S Anyhow, before we began the day's lesson, Mr. K showed the class the presentation and conference that was done yesterday afternoon with the lovely teachers in Saskatchewan. I thought it was extremely great how technology could be integrated with everything, which was the whole ball of wax about it. The conference was about how we mix education and technology, giving it a little FLAIR. [spelling?] :D
**NOTE, mentioned during the presentation were new forms of online communication, and possible DEV working methods, between members in a group!
GEOCACHING: a way of communicating being in the same space, but during different times.
DIMDIM: is a website, dimdim.com, in which a person can set up conferences to collaborate with group members without being in the same place. It's basically the opposite idea of GEOCACHING; meaning that people are communicating at the same time, but in different spaces.
TODAY'S LESSON: SLOPE FIELDS GALORE!!
The class started off by posting up the answers to our previous homework, reflecting on what we learned about slope fields so far.
 For example, without being too mechanic, I'll explain...well, the mechanics of the second slope field, where, dy/dx = 2x.
For example, without being too mechanic, I'll explain...well, the mechanics of the second slope field, where, dy/dx = 2x.The notation dy/dx shows that the equation is a derivative, and fits into the definition of a differential equation, where one variable is a derivative. 2x is an x dependent function, ergo, an x dependent derivative.
Then, we look at certain points on the axes, and determine what the slopes would be at that point. It is similar to plotting points on a graph, but instead using slopes within certain regions inside each quadrant. Once the grid is finally filled up with a variation of slopes, a "picture" is sort of painted.
The slope field takes the shape of a parabola. Now, mathematically, we know that 2x is the derivative of x2. But what always seems to be forgotten when anti-differentiating a function is always the idea of "+ C" at the end. This represents that A FAMILY of FUNCTIONS can be differentiated and still get 2x as the rate of change. The slope field depicts the family of possible parent functions.
Immediately after, we were given possible multiple choice questions that might make an appearance on the exam. These are shown on slides 4, 5, 8 and 9. Slide 9 is our homework, I believe, along with exercise 9.2.
The rest of the slides are pretty straight forward, with an exception of slide 5, and slide 8.

The only thing to be noted here, wasn't really because it was difficult, but it was worth noting. There was a specific pattern in this slope field, where the slopes are the same for a period, going in a constant direction, and all of the other slopes appear to be "bouncing" off of that "line" of slopes, then that line that slopes are bouncing off of is an asymptote. That was a really bad explanation. I can't quite articulate it correctly, but it's at the tip of my tongue.
As for slide 8...

This was one of those times when we got the correct answer, but we couldn't exactly explain how we got that specific answer, well not thoroughly at least. We mechanically knew what we were supposed to do, but the thought of how it works and WHY it works slipped our minds. Then it was time for. CALC. SCENE. INVESTIGATION.
Mathematically, the majority of the class massaged the equation by "finding the limit", making the denominator equal to ZERO. But WHY?!
REASON: Vertical segments are where the slopes of a tangent line, [derivative] are undefined and are therefore vertical, since a number is being divided by ZERO. That's the big whoop that we couldn't really fit together in class this morning. Once again, I'm sorry that my explanations are probably not up to par, but I am.. KABLUWEEE today. Nerves are kicking in, and my eyes are bloodshot. Too many things going on. I really don't like that this post is bland and what I don't like more is that I don't have much energy to read this over again and change it.
WOE IS ME.
As for the tradition that the class has recently started, I'm just going to embed and shamelessly advertise videos from youtube on this post. BECAUSE all I have to do is COPY and PASTE. The two most powerful commands a computer person could ever know.
I'm abusing this and posting 1, since they aren't necessarily FUNNY. It's just something that I'd like to learn. IN THE NEAR FUTURE. I just thought it was necessary to show the world what they're missing. :D
FIRST OFF. MEET SHAUNA NOLAND. Incredible flexibility. I call her ALIEN.
About 0:10 - 0:14 s. in this video. I've tried this, and have fallen with a loud THUMP each time. And sorry for the bad TV synch, it was the only embeddable one.
THIS ONE... TUTTING is an art form which I make look like doggy doo. Kristina will probably enjoy the chopsticks skills at the end. You know I conquer. LULZ.
Lastly, Francis, you're the next scribe.
Saturday, March 21, 2009
Slope Fields: Graphically
- AP Exam Practice Non-Calculator Quiz #3
- Introduction to Differential Equations (Cont'd)
- Slope Fields: Graphically
AP EXAM PRACTICE NON-CALCULATOR QUIZ #3

Since f'(1)=0, that means that when we integrate starting at x=1, we should integrate up to the point where the integration yields 0, to satisfy the condition that f'(x)=0. (Where else would f'(x)=0 besides at x=1?) We can see through symmetry that occurs at x=3.

To find P'(x), we differentiate P(x) via chain rule. Plug the numbers in to get P'(3) = 12. Straight-up application of chain rule.

It's given in the question that H(x)=f^-1(x). If we insert both sides of the equation into f(x), we get f(H(x)) = x, which is the key idea to solving the question. Use implicit differentiation to find H'(x). Solve for H'(x). Plug and chug.

Let's visualize the graph. sqrt(1-x^2) is the equation of a semi-circle, derived from the equation of a circle, x^2 + y^2 = 1, and x is a factor that distorts the perfect semi-circle when x is multiplied by sqrt(1-x^2).
Because the function given contains a square root function, we know that the function has a limited domain. (The radicand can't be negative.) So, the interval of the function is [-1,1].
Note that the question is asking for the total area, which means we make sure that the top area (above the x-axis) doesn't cancel the bottom area (below the x-axis). That can be avoided by taking the absolute value of the equation. But, in this case, if we graph x(1-x^2)^0.5, we see that the graph is symmetrical about the y-axis. So, we can instead find twice the area of one-half the semi-circle-like figure. Either way yields the same result.
To find the area underneath a function (integration), we antidifferentiate the function, in this case by integration by parts, and apply the fundamental theorem of calculus to get 2/3. This is shown on the slide in blue font.
INTRODUCTION TO DIFFERENTIAL EQUATIONS (CONT'D)

Continuing from our previous class' introduction to differential equations...
a) We know that a(t)=-32 ft/s^2 is the acceleration due to gravity. Antidifferentiating a(t) yields velocity. We know v(0)=-16. So, we know from the family of velocity functions (-32t+C) that we're pinpointing the -32t-16 function. Antidifferentiating v(t) yields s(t), the position function. We know s(0)=96. So, we know from the family of position functions (-16t^2-16t+C) that we're pinpointing the -16t^2-16t+96 function.
b) When the rock strikes the ground, the stone would stop on the ground, so the stone's velocity would be zero. v(t)=0 at t =-3,2, which is determined by finding the roots of the velocity function. We reject t=-3 because we designated t=0 when we dropped the stone. At t=2, s(t)=0, which is determined by plugging t=2 into the s(t) function.
c) Plug t=2 into v(t) to get v(2)=-80. (Refer to part b.)
SLOPE FIELDS: GRAPHICALLY
 dy/dx = y, meaning that the derivative function is the parent function itself and vice-versa, That's e^x. So, the slope is 0 at all the points on y=0. The slope is 1 at all the points on y=1. The slope is -2 at all the points on y=-2. The slope is 5/pi at all the points on y=5/pi. Etc. We drew the tangent lines at lattice points to easily visualize this field of slopes.
dy/dx = y, meaning that the derivative function is the parent function itself and vice-versa, That's e^x. So, the slope is 0 at all the points on y=0. The slope is 1 at all the points on y=1. The slope is -2 at all the points on y=-2. The slope is 5/pi at all the points on y=5/pi. Etc. We drew the tangent lines at lattice points to easily visualize this field of slopes.So, if a bird were to be at coordinate (0,1) and the slope fields were the direction the wind is blowing, then we can see the bird flying in the same direction as the wind in such a way that its trail can be seen as the graph of a function, which is shown in green.
HOUSEKEEPING
The rest of the slides are for homework.
Solution to 9.1 #9 is on the last slide.
The human rights assembly for The International Day for the Elimination of Racial Discrimination, hosted by The DMCI Human Rights Group, which we all enjoyed watching, is an assembly that occurs prior to Spirit Week. When Monday comes, Daniel McIntyre will enter the era of Spirit Week, a week of festivities hosted by Student Council, including Monday and Thursday period 2. So, Tuesday's scribe is .:. J + ME .:..
Spirit Week Themes
- Monday: Sports Day - Sports Obstacle Course
- Tuesday: Superhero Day - Save the Day Relay Race (you could dress up in a costume or wear a t-shirt that has a superhero logo on it)
- Wednesday: Twin Day - Talent Show
- Thursday: PJ/Crazy Hair Day - The Chris Frolic Comedy Hypnosis Show ($2/ticket)
- Friday: Colour Code Day - Grade War Gym Riot (gr.12s wear green; gr.11s wear blue)
Fortunately, this year's Student Council is carrying on the Daniel McIntyre tradition of having a hypnotist perform at our school. This only happens once every two years, and our graduating year just so happens to be that year! It's $2/ticket for Thursday, March 26 to see your friends get hypnotized. Proceeds may go to Grad Committee if enough fundraising is made.
This will also be Daniel McIntyre's last traditional 5-day Spirit Week. Let's make the best of it. =)
Friday, March 20, 2009
Thursday, March 19, 2009
A New Unit: Differential Equations
But apparently, it's something new, but something old. Like a nice pair of chucks. :)
We started with an equation to see if we could grasp the concept before he formally told us. So Joyce did this question for us. Basically what she did is she anti differentiated a(t) to get v(t). She determined C to be ten by setting v(0) = 10 so then the 0 made the first and second term in v(t) to be 0 so then C = 10.
So Joyce did this question for us. Basically what she did is she anti differentiated a(t) to get v(t). She determined C to be ten by setting v(0) = 10 so then the 0 made the first and second term in v(t) to be 0 so then C = 10.

 She then found the roots at 5 and 1 by factoring the function. v(t) = 2(t-5)(t-1). She stated the particle (Why are particles moving along x-axis' again??), changes direction at one and five, but Mr. K asked her to verify it. So she drew a graph, but he then again asked her how she could back that up, and she used the first derivative test.
She then found the roots at 5 and 1 by factoring the function. v(t) = 2(t-5)(t-1). She stated the particle (Why are particles moving along x-axis' again??), changes direction at one and five, but Mr. K asked her to verify it. So she drew a graph, but he then again asked her how she could back that up, and she used the first derivative test.
Why?
Because velocity is the derivative of position. So from negative infinity to 1, the function is positive, from one to five the function is negative and finally from five to infinity, the graph is positive. Therefore, the particle changes direction at one and five.
This is when thing's started clicking. We realized that..
Acceleration is the derivative of Velocity.
We realized this because due to the given values, they were all related to each other and they are rates of change of each other.
So we tried the theory and antidifferentiated velocity.
 This is when he introduced that these were differential equations, and introduced five words to us.
This is when he introduced that these were differential equations, and introduced five words to us.Order
General Solution
Initial Conditions
Initial Value Problem
So if there is a derivative of the equation and is represented by a variable, we call it differential equations. But wait! There's more. There's flavours but we'll get into that later.
Next are the order.
 Obsessive Pencil Ordering by mimi.amoure
Obsessive Pencil Ordering by mimi.amoureThe general solution is the family of functions, which is the function plus the vertical shift [ + C]
Initial conditions are the one value that picks a certain function from the family. Using conditions like v(0) = 10, which would pick out that one function from the whole family, like Tito Boy (Filipino Joke :P).
The initial value is determined by the initial conditions of the differential equations.
So learning all tha simple stuff, we were given a differential equation to solve given the intial conditions.
 So Justus did the courtesy of doing this question for us (which I assume everyone did correctly).
So Justus did the courtesy of doing this question for us (which I assume everyone did correctly).First the anti derivative of f'(x) was found and then we subbed in f(1) to find C to find the parent function. Pretty simple right? Yeah, I liked it too.
Anyways, zeph's the new Scribe. :)
Now to end it off with the new trend... YouTube Videos!!! I don't know how old school some of you people are, but I'm upset that they don't do re-runs of "Whose Line Is it Anyway?". Best Improv show I've watched.
One of my favourite episodes. XD
Wednesday, March 18, 2009
Bob
This unit is mostly about xolume, and who u can see the washer.
We looked volume by shell and slicing.
We learned a new way to find average value of a set of numbers.
This umit covers a lot of things that is kind of hard.
I try mu best to usr the rest of the morning to study and do good on the test.
Well, see u!!!
Hope every one do good on the tesr.
BYE!!!!!!!!!!!
Tuesday, March 17, 2009
Application of the Integral BOB
I hope I do alright and MacGyver it tomorrow. I'm actually cramming right now while trying to finish a bunch of other homework, so I'll see how it all goes.
Applications of Integrals Bobbbbb
So since I'm super tired, I'm kinda gonna cut to the chase, so I can get all my z's haha.
SO overall I found the unit wasn't to bad. I understand the concept of taking a slice of whatever your looking at, analyzing it, and applying what you understand about that slice to the rest of the solid.
I'm finding the hardest part to generally be figuring out what the solid looks like and what exactly the question is asking. I also tend to forget some bits of the question (like when dealing with washer problems, I sometimes forget to subtract the inner circle :P)
Anyways the final verdict, this unit wasn't that terrible, although it wasn't my favourite either.
K, well I'm off to sleep, good luck tomorrow everyone!
~Ciao
Scribe Meets BOB!
Yes, so I'm going to input my BOB in the same post also! So here I go!!! Also, what the heck is that ugly bar on my front slide? Oh well, whatever. I'm just glad slideshare finally worked.
Anyways, I thought this unit was pretty hard to grasp at first, especially the rotation parts. I couldn't see how they made the washers and shells at first but after doing lots of practice with them, I can see the patterns! They're beautiful by the way. Yes, so the pre-test also gave me some confidence for the test tomorrow since I did pretty well. Although, I kind of blanked out and couldn't finish my long answer. I basically just left the integral but didn't go on with solving for k. Silly me, har har. I won't do it for the test though.
As for the hardest parts for me. It is definitely the density stuff like that Boston by the Sea question we took so long to finish. Although I'm still kind of iffy, I think I'll manage.
Yeah, so in case you didn't look through the slides, the next scribe is Lawrence.
And to follow with the recently started tradition, here's a youtube video. I'm in a massive nostalgia stage right now, heck, I even watched the first episode of the first Power Rangers again when I got home today. Great stuff man. Anyways, here's my contribution...its a bit of what's to come...if you catch my drift >_>
BOB on Applications of Integrals
We started out by just finding simple distance and displacement given a specific scenario or problem, sure this was easy but then we moved to revolving 2d graphs.
In my opinion these graphs have no business revolving whatsoever. This was just confusing. We revolved these graphs on various points all over the plane, and certain points caused the shape to be a washer or cylindrical shell which required a few more calculations.
Good luck on the test everyone. I'm off to bed.
BOB The Builder indeed. BOB the Integrator.
Anyhoooooo. Back to business. **cough**. I think for me, this has been the unit that took me the longest to understand. The beginning was easy, it was direct integrating, and was understandable. But when 3D shapes are coming from 2D areas rotating around the cartesian plane, things get a little more complicated.
I think what was the hardest for me was trying to figure out which method to use, and the fact that I didn't quite understand why things were being done. I mean, I understood how to find the volumes and why the "patterns" were structured that way, but there are those word problems that I seem to have trouble with. It's like I understand how to do it, yet, I get stuck somewhere. I can't seem to finish one whole question like that without someone holding my hand, even if I'm almost on the last step. I also tend to make A LOT of errors. I'm a whole error . haha. But yes. That's me.
As for what I was saying earlier, I sometimes read the problem and it doesn't seem to click in my mind what I'm trying to find. It's like I'm going in circles. Mr. K says it's easier to know what we're trying to figure out with a diagram, but most of the time, I draw it incorrectly. That's what I've been working at for the past few days, and I know I should have done it earlier, but there are just too many things going on in my head right now. I'm not trying to make excuses, and I'm sorry if my non-responding vessel seems to bug you, Mr. K. I'm trying.
But yes, just like other tests, I only have a sliver of confidence in me, and so far, from what my marks are probably saying, I'm a "failure"...but it still doesn't stop me from trying to go up. :)
But yes, like all of my other posts, this one seems to be droning on, so I shall cough my way back into the textbook and slides on the blog.
BOB
BOB Version 8: Applications of Integrals
The visualizing of the washer and our quest in search of the hole took a lot of time for me to wrap my head around. Determining the integral of a function that's rotated around a line besides the x- and y-axis kinda messed me over in the pretest, but I managed to re-learn some of it thanks to the collaboration.
But when The Mean Value Theorem of Integrals came along, it was like a break from all this revolving and rotating, which made my head revolve and rotate too, not in the literal sense.
I realize I have to emphasize working more on the density problems since when Mr.K said "this should be a gimme!" it wasn't really a gimme as of yet.
You have reached the end of my BOB.
BOB for the Application of Integrals
This is my BOB.
This unit was quite interesting. I never would have thought that you could rotate anything on a Cartesian Plain. The first few sub-chapters on rotation around the x and y axes were quite tough at first. I couldn't see what was going on. But later on I began noticing how the solids would look like. Then when it came to calculations, imagining one sample slice of that solid made it easier to create an integral to find the Volume of the solid.
The last sub-chapters on the density-related functions were the hardest part of this chapter. I didn't do the homework that I was asked to do because of other priorities (Sorry Mr.K) but I did read a bit in the text which helped me understand a bit. I am certain that there will be at least one question that is related to this sub-chapter on the test and AP exam.
That is my BOB and good morning.
Monday, March 16, 2009
We suppose do the pre-test to day, but we are confused at certain type of question so we continued on this question:


This is the homework from Friday.

Use trapezoid sum to answer this question part a.

For part b, u basically just plot the graph out and u find it's constant at 1 to 8 so it's a straight line there the equation is -7.5r=82.5.
0 to 1 is also constant no change in slop so it's 75.

The 2ND question: draw the diagram 1st.
each one is 5 units away so it's d(0) to d(20).
then you add all of them up, it's underestimate you can tell from the graph.
I didn't really remember what we had went through in class.
Couple things to remember for this unit.
* always take a piece out of the whole solid, no there it's a disk or shell.
*dx is always means something, don't just put it in because u have to.
some helpful links to help review for the unit test:
http://www.intmath.com/Applications-integration/Applications-integrals-intro.php
http://www.mecca.org/~halfacre/MATH/appint.htm
http://education.yahoo.com/homework_help/math_help/problem_list?id=minicalcgt_6_1
hope this helps!!!!
the rest of the slides are home works to practice.
By the way next scribe is ........Kristina..............
Saturday, March 14, 2009
HAPPY PI DAY EVERYONE!! It's.. OFFICIAL!
As for today.. No pie. Thankfully. No more tummy aches...and no more me, yelling "KEY LIME, WHERE'S THE KEY LIME?!?!" Although I'm grateful that I got peach pie.
**giggle.snort.** I couldn't resist. I was.. after all.. watching it all day. I know he's going to be celebrating Pi Day.. I feel like calling it National Pi Day. Is it national?
That video isn't any comparison to the nostalgia and the nom nom. So.. I have yet to conquer.
As well as devour pie, we had a little chit chatter here and there, while Mr. K took pictures of the pies and people... **wink wink** send them over, Mr. K. xD Memories.
Afterwards, we ate more pie drank some chocolate milk and/or soda, I gained at least five pounds, I did a few pirouettes in the classroom, since.. I never get to do them in math class. But I can't even do ten anymore.. I've lost my centre...too much pie :S And then we discussed a topic along the lines of how today's advanced technology affects both the learning experiences of students and teachers. Mr. K asked if there were any volunteers to do a live chat in a couple of weeks, as well as record our feedback on his nifty little mp3 player. I still wonder what's on it...It's what I think about every time I see someone with an mp3 player or an iPod.
Later in the class, we drew our little pi signs. Pie signs... I don't know anymore. After we "painted" our masterpieces with pencils and highlighters, Mr K. flaunted his environmentally friendly Mac to take his pictures. I feel like I've already said this earlier in the post.... erm...uh. Oh well. If I had had the time, I'd probably draw something along the lines of....
 That's all I seem to remember from Friday's class. I'm just going to say, that I'm really happy with where we're going in calculus right now. We're working hard and getting prepared to brace ourselves with the exam. If we keep this up, we all could probably ace this. At least you guys, as for me? I'll try my hardest xD
That's all I seem to remember from Friday's class. I'm just going to say, that I'm really happy with where we're going in calculus right now. We're working hard and getting prepared to brace ourselves with the exam. If we keep this up, we all could probably ace this. At least you guys, as for me? I'll try my hardest xDREMINDERS:
- Pretest will mostly fall on Monday's class.
- Test on Tuesday if all goes as planned.
- Next scribe is yinan
Hope you enjoy the remainder of *National* Pi Day!! Gooo out, get some pie. I really wish there was a steak day. Or an onion rings day... **drool** PARTYYY!!

Friday, March 13, 2009
Happy Pi Day!

Wishing you the best of Pi Days!!!
Did you know that the U.S. House of Representatives even passed a resolution calling for March 14 to be recognized as "National Pi Day in the United States? You can read about it here.
Photo Credit
Not Paul After Work But Before Pi Day Scribe Post EXTRAVAGANZA (oh and we did some math or something)
Digital Ethics: Or How I Learned To Start Worrying And Think About My Online Identity
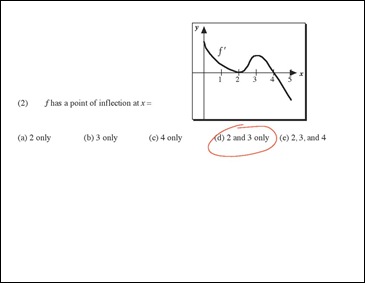
So today as usual we did our little “AP Exam Practice Quiz.” This one was, in my opinion, easier than the earlier ones because half the quiz was just about the 1st and 2nd derivative (I note though that I got these questions wrong too so hah).
The aforementioned questions are these:
So the first question is just asking you for local minimums. Just by looking at the graph, we can sort of rough out a sketch of the original function f (shown here in red). And that’s all we really need! Just by looking at our rough sketch we can say the original function f has local minimums at f = 5 and f = 0. Remember, we’re talking local not global minimums. In fact, unless your graph is always decreasing or something, your bound to have min/maxes at the beginning and end of a graph. Good thing to remember.
In this question, things get even easier. A local max or min on the first derivative is a critical number on the second derivative. 0 and 5 dont work, but 2 and 3 sure do. 2 is an inflection point, although not a local max because the second derivative keeps increasing. 3 is where the second derivative hits a local max and starts going downwards (decreasing).
If anything, this would be the trickiest question, because you have to remember the relationship between Velocity, Acceleration and Position. Velocity is the anti-derivative of Acceleration, and Position is the anti-derivative of Velocity. Remember to use the given values to find C so your equation matches the ones given. Otherwise, a cakewalk. Remember, Physics and Calculus are almost the same thing, seeing as Calculus was developed to advance Physics.
This is all stuff we should know. Anti-deriving, use of the Fundamental Theorem, algebra. If you’re really stuck or lazy, your graphing calculator can even do the question for you. Math, 0 is the equation solver. Either input the equation into the solver directly or put it in the graphing variables then select Vars, Y-Vars, Y1. Let it do its magic. Seriously Mr. K, in the future we’d like to know this sooner.
Either before or after the Practice Quiz, Mr. K also had a little bit more of a talk with us about Digital Ethics and our online identity. He reminded us that nothing “disappears” on the internet, and that online, what goes up stays up. He reminded us to keep in mind how the content we create now will always be there and to be mindful of how that content will be perceived in the future.
Mr. K even suggested that a great graduation present would be our own domain name, which I totally agree with. Comon! http://paulsantos.com/ isnt even taken yet!
Anyway, after that we continued work on the Greater Boston question. We determined that this question was different in a few ways, namely:
- That we cannot use the Fundamental Theorem because delta r cannot be changed. Since we cannot make r infinitely small, we cannot integrate it, and we have to use a Riemann sum.
- That we should “integrate” from 1 to 8 instead of 0 to 8 because the value doesn’t change from 0 to 1. Instead, we'll just add that extra population.
- That unlike our previous cylindrical shells questions, we’re dealing with half a shell not a whole shell.
The class ran out of time, and so we were left to ponder the population of Greater Boston by the seashore another day.
The homework was the remaining questions for 8.5 as well as finishing the Greater Boston question.
Happy Pi/Pre-Test day guys, see you tomorrow. Jamie, cant wait for your cheese cake. As a reward for making such delicious food, I pass the scribe torch onto you.
And some extra value added content to make this scribe post a delicious and nutritious part of your daily scribe serving:
Falcon Pawnch:
Good night guys. Hopefully I'll wake up in time to pick up some delicious blueberry pie.
Thursday, March 12, 2009
Wednesday, March 11, 2009
Boston Bay problemmmsss
Anyways enough griping, what we did today. To start, we had another little quiz. I'm not really quite fond of these things, although I suppose they're good tools for both Mr.k's and our own assessment of where each individual student is/how well they're doing in the course. As usual we had four questions, and this happened to be one of the no calculator varieties.
So onward with the first question.

So in this question, your given the graph of f(x) and asked to find some information (specifically, which of the 5 points f'(x) < 0 and f''(x)> 0. This for the most part is testing to see if you know what the first and second derivative tell you about the parent function (namely that the first derivative tells you weather the parent function is increasing or decreasing, and the second tells concavity.) Knowing this we find that solving the problem is a simple matter of looking at the concavity around the point, and if at that point on the parent function, it is increasing or decreasing.
Second question

This question 100% wont be on the exam
Why?
Because it's way to simple to be on the exam.
quote endquote of the conversation involving this slide. Pretty much, you just do the red in the picture, take the value of f(x) at 4, subtract is from the value of f(x) at 1, then put that over 4 - 1, then voila. answer. (in this case 4/3)
Neeexxxttttt

This question was also somewhat easy. If you read through the question properly you'll find it's just a direct application of the chain rule. Simply follow the values on the chart, plug em in, and away you go.
FINAL LAP!
dundun dundundun dundeedee!

SO, this one turned out to be a related rates sort of question. The first step here was to write the formula for the volume of a sphere, then differentiate that. Then, you simply begin plugging in some values (namely, a value smaller then 1 and one bigger then one) What you find is that with values of r smaller then 1, the sphere decreases in size, and that with values of larger then 1, the sphere increases in size. Turns out, this is one of the answers. yippee :]
Okay so this is where it gets kinda foggy, so please bear with me guys D:

So this question here, is basically a continuation of the stuff we were doing yesterday, with the funky density questions and the latter rho (whoa Iknorite?). Benchmen showed us the light with this one, so props to him for that goodness.
So in part a.) we need to write a function which will give us the number of cars. We know that the function given describes the traffic in terms of cars/km. To find cars we need to multiply this my Delta km (change in km.) Now as bench said we're actually trying to get really small changes to Delta km ends up ad just dx. (As Shown on the slide)
After all that we put it back together, and find that to find the number of cars, you just do this. (its kinda hard to explain in words so I just cropped it xD)

The next bit of the question (aka. part B.) goes something like this.

Quite simply, all you do is evaluate over the interval 0 to 30 (since you have 30km of road your working with.)
Alrighty guys, its not time for the post titled, BOSTON BAY PROBLEMMMM
dum dun dundundundun.

Now, instead of tackling this whole thing at once, lets start with just part a (or what we started of it anyways before the class ended D:)

So, from what I can tell by looking at the blog, we got as far as setting up the units, (aka, out delta whatever, that becomes the dx.) I'm pretty sure it was around this time the bell rang, and we got our homework and things.
Okay everyone hopefully that wasn't a nightmare to follow, if it was, I apoligize, thats what I get for forgetting my books -_-;
So ja, the next scribe is Paul because I havent picked him in awhile lol.
Ciaooooo
edit: Btw, homework is 8.5 6-10 and the rest of the boston bay problem :]
edit edit: Soo I couldn't leave without some goodness haha