Evaluating the Value of the Intermediate Value Theorem of Integral Values

Hi everyone,

I almost forgot to scribe, but thanks to a friend I remembered.

Today we had an AP Multiple Choice Practice Quiz. It contained 4 multiple choice questions and calculators were allowed. Beforehand Mr.K calculated the average time a person has per question on the calculator section of the multiple choice questions. We had approximately 12 minutes for the 4 questions.



Above is the first question. It is a Linear Approximation question. These type of questions require you to find the equation for the tangent line that is tangent to a point on a function. Then use that line to approximate the derivative of a nearby input. So to find the equation of a line, you need a point which is given and a slope (derivative at that point) which is also given. So place the numbers into the Point-Slope form of a line, with the derivative as a slope and the coordinates as x_o and y_o accordingly. Then using that new line equation input 3.02 into the line function and solve.



The second question involved understanding the term changing direction when given a velocity function. In a displacement function a change in direction would mean the function is increasing then decreasing or vice versa. So when a displacement function is increasing the derivative is positive and when it is decreasing the derivative is negative. So that means the change in direction can be found where ever the derivative function crosses the x-axis (has a zero). Most of the class had a problem on this question because we were not paying attention to the interval.



The third question involved our good friend, the Mean Value Theorem of Derivatives. The Mean Value Theorem says that if you make a secant line connecting the endpoints of a continuous and differentiable function in a closed interval, there is at least one other point on the function that has the same slope as that secant line. So the first step in solving this problem is to find the slope of that secant line. Find that is simple, find the change in f(x) and divide by the length of the interval. Now that you have the slope, differentiate the given function and set it equal to the slope of the secant line. We do that because we are trying to find another x-value that has that slope. So just solve for x and you have an answer.



The last question involved Implicit Differentiation. Implicitly Differentiate the given algebraic equation, remembering that derivative of a constant is 0. Now solve for y'. To find y' we need an x-value. To find that plug the given y-value into the given equation and solve for x. Now plug the given y-value and the newly discovered x-value into the differentiated function and solve for y'. Now you have the answer.

After that little quiz, we continued on the Intermediate Value Theorem of Integrals. The theorem says that on a continuous function, f, within a closed interval, [a,b] there exists an input between a and b, such that the signed area under the function, f,is equal to the area of the rectangle under the line, f(c), between a and b. I don't know if that is the right way of saying it, but that is how I see it. Correct me if I am wrong. I hate doing this but here is the formula...



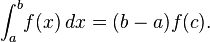
So we use that theorem to find the value of c in the following slides.

The final slide has a problem involving the Fundamental Theorem of Calculus. It says that if you integrate a function from a to b, the answer is the change in value of the function, f(b) - f(a). So that makes sense, we are given a rate of change, and in this case the rate at which oil is leaking. So when we integrate the function for the first 10 hours we get a number, and that number represents how much oil has leaked out.

That is it. Watch the video at the end of the slides for a little review on the Mean Value Theorem.

We will be continuing our discussion on the Intermediate Value Theorem of Integrals tomorrow, I believe.

Next Scribe will be Joyce. (Sorry for the confusion on my last scribe post)

Good Night and may the force be with you.