Digital Ethics: Or How I Learned To Start Worrying And Think About My Online Identity
So today as usual we did our little “AP Exam Practice Quiz.” This one was, in my opinion, easier than the earlier ones because half the quiz was just about the 1st and 2nd derivative (I note though that I got these questions wrong too so hah).
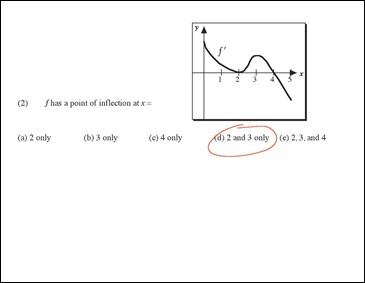
The aforementioned questions are these:
So the first question is just asking you for local minimums. Just by looking at the graph, we can sort of rough out a sketch of the original function f (shown here in red). And that’s all we really need! Just by looking at our rough sketch we can say the original function f has local minimums at f = 5 and f = 0. Remember, we’re talking local not global minimums. In fact, unless your graph is always decreasing or something, your bound to have min/maxes at the beginning and end of a graph. Good thing to remember.
In this question, things get even easier. A local max or min on the first derivative is a critical number on the second derivative. 0 and 5 dont work, but 2 and 3 sure do. 2 is an inflection point, although not a local max because the second derivative keeps increasing. 3 is where the second derivative hits a local max and starts going downwards (decreasing).
If anything, this would be the trickiest question, because you have to remember the relationship between Velocity, Acceleration and Position. Velocity is the anti-derivative of Acceleration, and Position is the anti-derivative of Velocity. Remember to use the given values to find C so your equation matches the ones given. Otherwise, a cakewalk. Remember, Physics and Calculus are almost the same thing, seeing as Calculus was developed to advance Physics.
This is all stuff we should know. Anti-deriving, use of the Fundamental Theorem, algebra. If you’re really stuck or lazy, your graphing calculator can even do the question for you. Math, 0 is the equation solver. Either input the equation into the solver directly or put it in the graphing variables then select Vars, Y-Vars, Y1. Let it do its magic. Seriously Mr. K, in the future we’d like to know this sooner.
Either before or after the Practice Quiz, Mr. K also had a little bit more of a talk with us about Digital Ethics and our online identity. He reminded us that nothing “disappears” on the internet, and that online, what goes up stays up. He reminded us to keep in mind how the content we create now will always be there and to be mindful of how that content will be perceived in the future.
Mr. K even suggested that a great graduation present would be our own domain name, which I totally agree with. Comon! http://paulsantos.com/ isnt even taken yet!
Anyway, after that we continued work on the Greater Boston question. We determined that this question was different in a few ways, namely:
- That we cannot use the Fundamental Theorem because delta r cannot be changed. Since we cannot make r infinitely small, we cannot integrate it, and we have to use a Riemann sum.
- That we should “integrate” from 1 to 8 instead of 0 to 8 because the value doesn’t change from 0 to 1. Instead, we'll just add that extra population.
- That unlike our previous cylindrical shells questions, we’re dealing with half a shell not a whole shell.
The class ran out of time, and so we were left to ponder the population of Greater Boston by the seashore another day.
The homework was the remaining questions for 8.5 as well as finishing the Greater Boston question.
Happy Pi/Pre-Test day guys, see you tomorrow. Jamie, cant wait for your cheese cake. As a reward for making such delicious food, I pass the scribe torch onto you.
And some extra value added content to make this scribe post a delicious and nutritious part of your daily scribe serving:
Falcon Pawnch:
Good night guys. Hopefully I'll wake up in time to pick up some delicious blueberry pie.





1 comment:
Wow what a nostalgic video. I feel older now
just remembering the times I used to play that one with my brothers back in the day lol XD
Nice scribe btw :D
Post a Comment