Well, we did section 2.5 Critical Numbers; Relative Maximum and Minimum Points.
We start off with the local maximum and the local minimum.
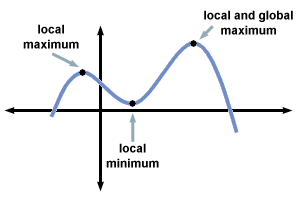
A local minimum, also called a relative minimum, is a minimum within some neighborhood that need not be (but may be) a global minimum.
A local maximum, also called a relative maximum, is a maximum within some neighborhood that need not be (but may be) a global maximum.
Global minimum is the smallest overall value of a set, function, etc., over its entire range. It is impossible to construct an algorithm that will find a global minimum for an arbitrary function.
Global Maximum is the largest overall value of a set, function, etc., over its entire range. It is impossible to construct an algorithm that will find a global maximum for an arbitrary function.
As x^2 is increasing, 2x is also increasing.
Critical Point is where f'(c)+0 or does not exist.

Then we did Example 1 on page 115.
Homework for today is 1,7,9,11,15,19,22,23,25 on Exercises 2.5
I'm done! next scribe is Yi Cong ( good luck! ^_^)

No comments:
Post a Comment