Thursday, October 30, 2008
October.30th 2008
We get to read through the section and figure out the examples on our own.
Most of us did example 1 Determing cost from changing price rate.
Well the question and the solution is in the text book page 181.
Dr. Eviatar said that we will keep doing this chapter tomorrow.
Monday is the pretest, and Tuesday will be the test of chapter 3.
I'm done! The next scribe is Shelly
ps: Happy Halloween for tomorrow ^_^
Wednesday, October 29, 2008
Introduction to the Fundamental Theorem of Calculus
∆y/∆x = [s(4)-s(1)]/(4-1) = [(4^2-3*4+1)-(1^2-3*1+1)]/(4-1) = 2
The question is asking for the change in position, which is the slope. Since time is the independent variable and position is the dependent variable, the derivative of the graph is the velocity, which is the slope.
2. Suppose a car is moving with non-decreasing speed according to the table below:
t (sec) 0246810
speed (ft/sec) 303640485460
a) What is an upper estimate for the distance traveled in the first 2 seconds?
36*2 = 72ft
b) Determine upper and lower estimates for the change in position for the first 10 seconds.
Upper estimate = 36*2+40*2+48*2+54*2+60*2 = 476
Lower estimate = 30*2+36*2+40*2+48*2+54*2 = 416
b
∫y’dx = change in y over the interval [a,b]
a
The definition of the Fundamental Theorem of Calculus is on Slide 6.
http://apcalc07.blogspot.com/2007/10/todays-slides-october-25.html
http://apcalc07.blogspot.com/2007/10/thursdays-post.html
END NOTES:
3.4
Chapter 3 Pre-Test and Test is postponed to next week.
Next scribe is Yinan.
Tuesday, October 28, 2008
Workshop
First off, we were given a table of values, and we had to plot them on the given graph (I honestly don't remember those values.)
Next we were asked to find the lower and upper limits. Which were around 17.1 and 23.1?? ... Or something like that.
Then we were to estimate what the exact area was. I believe mine came up to around 19-something. Anyone else get the same thing?
Next we were to use different functions on our calculator to find the answer.
First question was to use the RIEMAN Sum program. I got a sum of 12.06.
When you use the program this is what you input:
LEFT: 0
RIGHT: Pi
X CHOICE: 0
NUMBER 10 <--- This is the number of subintervals
The next one, we were to use fnInt. The way this one works, is that you have to input the equation given to you in Y1.
Then input it like this fnInt(Y1, X, 0, Pi) *To put in Y1, press Vars, move right to Y-Vars and select Y1. Inputing this in simply as Y1 using Alpha will create an error.* For this one I also got a value of 12.07
The last one we were to use the 7th option under the Calc menu.
A graph would show up (because the equation is in Y1 already) and we were to use endpoints 0 and Pi. So you would choose X = 0 as the Left endpoint and use X = Pi as the right end point. After that, press enter and you should get a value around 12.07
And that's all we did today. So I guess the next scribe will be... Zeph!
Scribe List
kristina zeph yíNAЙ |
|
|
Quote of the Cycle ;
"Knowing is not enough; we must apply.
Willing is not enough; we must do."
Rence ~ Out
Monday, October 27, 2008
TEST RESULTS/REVIEW
Anyhow, I can't really re-explain the answers of the test considering that these tests were probably "recycled", so what I'll do is give reminders and notices for the important dates coming soon in class and maybe recap what I've learned in this chapter so far. So I won't have to guilt trip myself into scribing one more time. I'll...compensate for it. I guess that's the right terms for it.
IMPORTANT DATES:
Nothing really comes to mind except the likely test we will have on Friday this week. Happy halloween. That's what makes it so scary. Not the gore, the blood, or the costumes; it's the tests.
.:. J + ME .:.'s REVIEW OF CHAPTER 3 [I'm warning you..not to rely on this, it's probably not very informative. I'm just doing this to see if I understand this stuff or not. It's an effort, right? Wow.. whatever happened to my skills in English? I'm writing so informally. **sigh**]
3.1 CALCULATING DISTANCE TRAVELED
This is the first part of the chapter which acts as a link between the concepts of the previous chapter 2 and preparation for what will be taught further into the unit.
We discover that both integrals and derivatives have direct relationships with each other given that a derivative is a rate of change involving velocity and integrals involve determining the distance traveled, which is basically the area of the region below a function.
This chapter is easily explained remembering the idea of
distance = velocity x elapsed time.
3.2 CALCULATING AREAS: RIEMANN SUMS
This chapter focuses more on approximating the areas of rectangular regions below the functions and also parts of the regions above the function.
To find these areas, we take the limit of these approx. sums and find the area using the measurements of the intervals and the height of each interval that touches the function. The smaller the intervals are, the closer we are to being more exact in our approximates in area.
The name RIEMANN sums is just the name assigned to classify the method to find these sums.
Of course we have to take into account inscribed [below] and circumscribed [above] rectangles since, they do not fill in the spaces exactly.
Especially when looking for Riemann sums using something as obscure as a calculator, it makes it easier when we look for subintervals and choose midpoints [or left or right endpoints], so that it is easier to find what are known as RIGHT HAND SUMS [above fcn] and LEFT HAND SUMS [below fcn].
3.3 DEFINITE INTEGRALS
In this part of the chapter, a variation of the sigma notation is introduced, something that looks like a squiggly line. How fun to illustrate. But the subscripted and superscripted values are the coordinates of the main interval, represented by [a, b] in the examples. We are still finding the sum of course, and it is the sums within the vicinity of of the main interval given. There is an infinite amt of limits of the number of intervals between [a, b].
I'm a bit choppy on this part still, so I'm sorry. I don't want to mislead anyone.
Monotonous Functions: are functions that either increase or decrease, but never go both ways.
Non-monotonous Functions: These functions are capable of increasing and decreasing, resulting in an "unpredictable" function and thus, it's intervals that don't follow a specific pattern.
Well that's all from me tonight. Ummmmm. Who shall be dubbed the next scribe? Rence, I guess.
With great power comes great responsibility. - UNCLE BEN. haha wow. when will that ever get old?
Sunday, October 26, 2008
Definite Integrals
We started off the class talking about Riemann and his sums. The Riemann Sums was the term given to the sum of the different areas of the graph between each interval that we created during the last few classes with M(r)s. Karras and Dr. Eviatar. More info about Riemann and his sums can be found in the link on the first slide.
Now onto the Integrals. We were introduced to a new notation called the Definite Integral Notation. It is supposed to be a funky looking Sigma notation with a few twists. In the notation it shows the main interval [a,b] in which we are finding the sum, the function being used, and the size of the intervals between the closed larger interval [a,b]. So the definition of this notation involves limits where the number of intervals between [a,b] is to an infinite amount. Since it is human impossible to do this (Nothing is impossible if you BELIEVE) we try to get as close as possible.
Okay to work with this notation we locate the section of the function in which we are investigating. The definition of the notation is to get the sum of f(x) multiplied by the change in x up to the nth interval. If you remember from previous classes, the more intervals that we include in our calculations lead to a more accurate estimation of the integral of a function.
We looked at a couple of examples in the next few slides and continued on to a bit of something new. Monotonous Functions are functions that either increase or decrease, but never both. These functions give us the ability to determine the margin of error in our estimations. This is because in Non-Monotonous Functions the margin of error will be useless because of the change in the rates of change. Since Monotonous Functions either increase or decrease they will have a error that can be determined. This error shows how many intervals are required to find the Integral. Depending on the function some might need more than others.
Homework is Chapter 3.3 and do questions 1, 2, 4, 5, 7, 11, 17. But do enough that you understand it. No point in doing too much or too little.
The next scribe will be .:. J + ME .:.
Good night and do not let the Cimex lectularii masticate your epidermis, imbibing your blood.
Friday, October 24, 2008
October 23rd: Return of the Definite Integral (sort of)
Today (or rather, yesterday if you want to be technical about it), we continued on yesterday's class about the definite integral. This time, instead of getting data from a table to find the mean of the upper and lower limits, we were provided with a function f(x) = x^2 and used that instead.
Tom Lehrer!
Thursday, October 23, 2008
Wednesday, October 22, 2008
Scribe List
kristina .:. J + ME .:. zeph yíNAЙ |
|
|
Note: Yes, I'm aware they are no longer in the class. I just have a case of nostalgia. Haha 8)
Quote of the Cycle ;
"Knowing is not enough; we must apply.
Willing is not enough; we must do."
Rence ~ Out
October 22. The Definite Integral
Today we started off my watching a youtube video entitled "Lobachevsky - Tom Lehrer" The video is about a mathematician named Lobachevsky who supposedly plagiarized from a fellow mathematician named Gauss.
Well back to the subject. We started out by graphing some values
 .
.The red bars represent the velocity or speed at the given time intervals as it changes gradually. The orange and green bars represent pretty much another graph, where the change in velocity was instant. Whether the change in speed was gradual or instant, we can't determine so. The curve in between the orange and green is the distance travelled, and this is what we will be trying to find.
We then try to find the lower limit by finding area of the lower limits (found in red bars).
Lower limit = sum of area of least possible #'s.
We multiply each value by the time interval (1).
Lower limit = 1.4(1) + 2.7(1) + 3.5(1) + 4.5(1) + 5(1) = 17.1 ft.
Don't add the last value, because this is the upper limit and it can't get any higher than this (t=5).
Now we calculate the upper limit, which includes the orange and green bars.
Upper limit = 2.7(1) + 3.5(1) + 4.5(1) + 5(1) + 5.7(1) = 21.4 ft.
Now estimate the distance by taking the average of these two areas. (17.1 + 21.4)/2 = 19.3 ft.
If we're talking about limits, the range would be 17.1 ft. to 21.4 ft.
At this point we find the ambivalent area (area of uncertainty) which is pretty much the orange-green bars. Ambivalent area = 1.3 + 0.8 + 1 + 0.5+ 0.2 = 4.3 ft.
We have an estimated area of 4.3 ft. under the curve which doesn't exactly match the previous results we estimated.
Now we decrease the time intervals to be more precise, and to see what happens.
 Let's find the lower limit, or left edge of this graph. Left edge = 0.7 + 1.35 + 1.5 + 1.75 + 2.05 + 2.25 + 2.4 + 2.5 + 2.7 = 18.2 ft.
Let's find the lower limit, or left edge of this graph. Left edge = 0.7 + 1.35 + 1.5 + 1.75 + 2.05 + 2.25 + 2.4 + 2.5 + 2.7 = 18.2 ft.Now we find the upper edge which is pretty much the same, but we exclude the number of least value and include the number of most value. It should equal 20.35 ft.
The distance will be between 18.2 ft. and 20.35 ft.
The mean distance is (18.2 + 20.35) / 2 = 19.3 ft.
The average distance remains the same as our last graph.
Therefore by decreasing the size of the time intervals we have brought both the upper and lower limits' ranges lower.
At 1 sec. interval range = 17.1 ft. and 21.4 ft.
At 0.5 sec. interval range = 18.2 ft. and 20.35 ft.
The mean stayed the same at 19.3 ft.
That was all we did in class, our homework is Exercise 3.1 questions 1, 3, 6, 7 and 9. Hope you enjoyed, if any issues, be sure to tell me and I'll be sure to correct them. The next scribe will be well, not Richard, but Not Paul.
Tuesday, October 21, 2008
October 21, 2008
Today in class we had our test on Derivative Functions, it was quite tough, because there were questions in there that we hadn`t reviewed before, but next unit should be easier.
That is all we did in class today, now you know why I wanted to be scribe.
The next scribe will be Joseph!
Monday, October 20, 2008
Scribe List
kristina .:. J + ME .:. zeph yíNAЙ |
|
|
Quote of the Cycle ;
"Knowing is not enough; we must apply.
Willing is not enough; we must do."
Rence ~ Out
The Pre-Test
Today we just had a pre-test and went over the answers. We were all in class, so I don't think I have to go over the answers in detail.
Answers:
1) A
2)D
3)C
4)D
5)D
6)
a)-2.25
b)f(x) = -2.25 (x-5.2) + 8.8
c)8.665
d)Negative
So by request, Francis asked to be scribe, for the same reasons everyone would want to be.
Therefore, Francis will be tomorrow's scribe.
Sunday, October 19, 2008
Scribe List
| |
|
|
Quote of the Cycle ;
"There is no such thing as good or evil...
Rence ~ Out
Friday, October 17, 2008
Friday's class of a couple Theroms.
We also looked at how to find zeros on a continuous function without our calculators. We were given an example on slide 2. f(x) = x3-3x+1. To find the zero of this function, we chose points [0,1] for this example. We then found out where the x-values were either positive or negative. On the example the point 0 was input into the function and equaled to 1. Which was positive ( f(0) = 0-3(0) +1 = 1). At the point of 1, the function was a equal to a negative number ( f(1) = 1 -3(1) + 1 = -1). Now we know that the zero of the function will be in between those two points. Now we want to hone in on a smaller region, so we should cut that interval of 0 to 1, in half. So we find the f(1/2) and see if it's positive or negative, so we know where to look next. The function of f(1/2) turned out to be negative, as found on the slide. We then know to look between points [0 and 1/2] because the zero will be in between a negative and positive value. It's best to divide the section by half to cover greater amount of space between the points. The next point we used was 1/4. We input this into the function and found it to be positive. Now we can look between points [1/4 and 1/2]. We then used the point of 3/8 in our function, which is in between our given points. It turned out this was negative, so now we know our zero is between 1/4 and 3/8 which is small enough of an interval where our zero is found, so we stopped there.
The next theorem we used was entitled the "Extreme Value Theorem". This states that on a continuous function, it will always have a maximum and minimum and will be an extremum value from where all points on the function will either larger or smaller depending if its the maximum or minimum extremum. Lets say that on a continuous function on interval [a,b] there exists numbers c and d where all x-values in [a,b] f(c) ≤ f(x) ≤ f(d). d will be the maximum and all x-values will be less that or equal to d. c is the minimum and all x-values will be greater that c or equal.
That's all we did in today's Calculus class. If anything is wrong, talk to me and I'll be sure to change it. The next scribe will be Lawrence!
Thursday, October 16, 2008
Continuity, and some more Limits

This image is basically a modified version of the first slide. Now this example was used to explain the concept of continuity. If you look at the image, I've drawn 3 sets of lines, the magenta (purpley) ones, the maroony ones, and the aqua ones. If you try to travel from one aqua line, to the other, you can do it easily, and without any kind of sudden changes. Therefore the graph is said to be continuous along that interval. The same goes for the magenta. However, when trying to travel from one maroon line to another, difficulty arises. At x = 0, there is a sudden change in direction, the line is no longer continuous, and there is now said to be a discontinuity. It is called a discontinuity because there is no way to get from one maroon line to the other in a continuous fashion. The next point we got into, were 3 defining rules of continuity, which I shall type out
here for everyone to see.
Continuity
A function is continuous at x = a if;
1.) lim f(x) exists
x->a
2.) f is defined at a
3.) lim f(x) = f(a)
So after going over these rules, we got some examples on the board, so we might get a better understanding of what each means.
For the first we came up with the following
1.) Example: lim f(x) = 1/x
x->a
Counterexample: (look at slide)
So as seen in this slide image here, the example graph produces a nice, rule following reciprocal graph (reciprocal of the graph f(x) = x), whereas the counterexample gives a piecewise function, which has that huge gap/jump/aka. Discontinuity at x = 10 approximately. Alright, moving on.
2.) Example: f(x) = x/2 at x = 1
Counterexample: f(x) = 1/x at x = 0
In the second example there, it is pretty obvious to see what the problem is. In the counter example, the function is NOT defined at x = 0 because you are then dividing by zero, and we all know how much fun that is. In the example however, all is good and well, and f is defined at a, as required to be continuous.
3.) Example: lim 1/x = 1 = f(1)
x->1
Counterexample: (check slide)

Okay, so the counterexample in this one, might seem a little confusing but I'll try to explain it as best as I can. Basically, its saying that f(x) = x2 when x does not equal 2; When x DOES equal 2, then f(x) = 5. Thus you get the graph with the weird point floating in the air. This point also leads to that magical thing called a discontinuity again.
Now it was at this time Dr. E said to checkout Pg's 140-141.
The final little tidbit in the lesson involved continuity on an interval, which basically says that if function is continuous from points a, and b, it is continuous on that open interval a to b. This is shown in more detail on the following slide
 The lim f(x) = f(a) basically means that starting above a and moving towards it, the function
The lim f(x) = f(a) basically means that starting above a and moving towards it, the function
x->a+
is continuous. The opposite is true for the lim f(x) = f(b) which says that starting below b and x->b-
moving towards it the function is continuous.
Now thats about it for my scribe post for today. I know we did a couple other things, (two slides), but I forgot my textbook at the school, and I didn't really understand them at all, so if someone could help out with that (ie by talking about it a little bit in their post, that would help me tremendously, and I could then go and fix mine.) Either way, like I said, I will need to get my text to help me explain those two slides.
So I think thats everything, which only leaves choosing the next scribe. I've decided it will be francis mkay. kay.
OH And I almost forget, theres alittle note about pg 143 here in my notes, which means it's probably a good idea to check that page out. As far as I remember there weren't any questions assigned for homework for tonight though.
Anyways I'm off, because I have lots of other things to do now. Hopefully my post made enough sense, and I apoligize for any discontinuities in it; feel free to point those out btw, so I may fix them.
ciao
Wednesday, October 15, 2008
Hand out
page 1
page 2
page 3
page 4
As we head into something new, this handout of Algebraic Limit Rules is handy (which was given to us on Friday)
Limits and Functions
Suppose that limits

exist and let "c" be a constant
CMR (Constant multiple rule)
The limit of a constant times a function is the constant times the limit of the function
lim c f(x) = c lim f(x)
SR (Sum of Function Rule)
The limit of a sum is the sum of the limit
lim (f(x)+g(x)) = lim f(x) + lim g(x)
DR (Difference of Function Rule)
The limit of a difference is the difference of the limits
lim (f(x) - g(x)) - lim f(x) - lim g(x)
PR & QR (Product of Function and Quotient of Functions Rule)
PR: lim (f(x)g(x)) = (lim f(x))(lim g(x)) QR: lim (f(x)/g(x)) = lim f(x)/lim g(x)
Example 1:

Example 2:

Example 3:

Note:

The limits are the same but the function itself is different, for
f(x) = (x2/x-1 - 1/x-1) there is a discontinuity at x = 1
For more examples similar to these one look at example 2 and 4 in the Algebraic Limit Rules booklet.
Example 2
Example 4
Homework: Exercise 2.7
1-9 (odd)
14-27 (odd)
and 24
And now it is time for the ROFL corner!
Since the last riddle was a tad difficult, I'll give you guys an easier one, which means that you won't need a hint for this one. ;D
How many times can you take 5 out of 25?
And if that one is too easy try this one! (Sorry!! I don't have a hint for this one!)
What belongs to you, but is mostly used by others?
Have fun!
Finally the next scribe will be...... Hi I'm Justice!
Tuesday, October 14, 2008
Continuing From Last Class.
First you use the critical points that you found and plug the values into the second derivative test and you will find the local max and min.

Next you find all possible inflection points by making the second derivative equal to zero and solve for x.

After Figuring all that stuff out you solve for the original function and use the critical points that we have found for the x values.

Now you need to find out if it is concave up or concave down.
To find the that out you need to choose a value from the ranges and plug it in to the second derivative formula which is f ''(x) = 4 - 12x

Next you solve for f(x) but this time you use the infliction points that we found for the x value.

This next picture is a picture of the second derivative i think. it shows when the graph is concave up and concave down.

Well thats all for today tune in next time. Next scribe post will be featuring Shelly.
Rguy out.
Friday, October 10, 2008
OCTOBER 8: INFLECTION POINTS, CRITICAL POINTS CONCAVITY AND DERIVS REVIEW
- f is a continuous function located on a closed interval [a, b]
- f is differentiable on an open interval (a, b)
- If f '(x) is posve for the x values in the open interval, then f '(x) is INCREASING on the closed interval, [a, b]
- If f '(x) is negve for the x values in the open interval, then f '(x) is DECREASING on the closed interval.
- f (c) is the max value of the function on the interval given that f '(x) is less than or equal to f (c) or vice versa, which is shown in the next pt. [LOCAL MAX]
- f (c) is the min value of the fcn on the interval given that f '(x) is greater than or equal to f (c). [LOCAL MIN]

Wednesday, October 8, 2008
Tuesday, October 7, 2008
Scribe List
| .:. J + ME .:. |
|
|
Quote of the Cycle ;
"There is no such thing as good or evil...
Rence ~ Out
Slides October 7th
Monday, October 6, 2008
Oct.6th/08
Well, we did section 2.5 Critical Numbers; Relative Maximum and Minimum Points.
We start off with the local maximum and the local minimum.
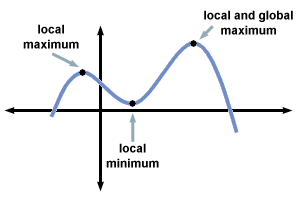
A local minimum, also called a relative minimum, is a minimum within some neighborhood that need not be (but may be) a global minimum.
A local maximum, also called a relative maximum, is a maximum within some neighborhood that need not be (but may be) a global maximum.
Global minimum is the smallest overall value of a set, function, etc., over its entire range. It is impossible to construct an algorithm that will find a global minimum for an arbitrary function.
Global Maximum is the largest overall value of a set, function, etc., over its entire range. It is impossible to construct an algorithm that will find a global maximum for an arbitrary function.
As x^2 is increasing, 2x is also increasing.
Critical Point is where f'(c)+0 or does not exist.

Then we did Example 1 on page 115.
Homework for today is 1,7,9,11,15,19,22,23,25 on Exercises 2.5
I'm done! next scribe is Yi Cong ( good luck! ^_^)
Sunday, October 5, 2008
Me and My TI-83.
On slide 2, we used the change in y / change in x to find the derivative. That method of course is where we find the slope of two points that are very close to the point we want which is where x =2.
On slide 3, the method we used is the quotient one. All we did with this question was to plug in 3 in x and chose 0.01 as our interval. From there we simplified and got the answer of 0.33. This is my favourite method for some reason. We also saw that we'd get the same answer with using the change in y / change in x way. After plugging in numbers like 2, 3, and 4 we noticed there was a pattern. The derivative for x=2 was .5, x=3 was .33, and x=4 was .25. Therefore, the derivative for ln(x) was 1/x.
From what we learned from Mrs. Karras, not all points are differentiable. The points that aren't are where the graph is....pointy! Like on the slide, the absolute graph is not differentiable at x=0. This is because the tangent slopes are -1 from the one side and 1 on the other side.
The other methods we learned were the dy/dx thing in our calculator and the nderive function in our calcs.
That's pretty muuuch it. *looks at scribe list.* The next scribe will be Yi Nan i suppose. Have fun scribing tomorrow. Now is time for me to enjoy the last hours of my weekend :(
Friday, October 3, 2008
Slides October 3rd
Thursday, October 2, 2008
The Power Rule...
The following image shows the equation work that was used to derive the rule. I will explain each line after the image.
 Line 1: Okay lets find the derivative of x to the power of n at x
Line 1: Okay lets find the derivative of x to the power of n at xLine 2: So we just throw it into the derivative formula like usual
Line 3: We have to expand the binomial in the brackets. There are 3 things to realize. First the first term will be x to the power of n regardless to what n is. Secondly, the next term will always have n as the coefficient and n-1 as the exponent and also multiplied by one h. Finally, every other term will have a unknown coefficient (this coefficient will become irrelevant and you will see later) and the exponent of h will increase by 1. So in the third term the power of h will be 2 and in the fourth it is 3 and so on
Line 4: Now we can get rid of x to the power of n because it is subtracted to zero by the other term.
Line 5: Now we factor out an h. Notice that the first term in Line 4 no long has an h variable in the term and every other term afterward still has an h variable remaining. This is the key to seeing the rule
Line 6: Now the h reduces and you are left with what was in the brackets in Line 5.
Line 7: Now we apply the limit and substitute all the h values with zero since there is no h in the brackets anymore. This will cause all terms containing the h variable to become zero. Since the first term does not contain an h variable, it won't be affected by the limit.
Line 8: This leaves us with the rule because all of the other terms are turned into zero thus not affecting the first term at all.
I hope this helped. If there is any more help required, please talk to Dr. Eviatar or myself for help...
Okay well I tried =P
The Derivative Function (Cont'd)
- Alternative Notations for the Derivative
- y = nx^(n-1)
- Derive f(x) = x^3
- Derive y = -1/x
Alternative Notations for the Derivative
f'(a) is the symbol used by Lagrange. E.g. If f(x) = x^2, its derivative is f'(x) = 2x.
dy/dx is the symbol used by Leibniz. E.g. If f(x) = x^2, its derivative is dy/dx = 2x.
y = nx^(n-1)
Then the Benchmeister took over the class and starting teaching us. He taught us a shortcut in finding the formula of a derivative by using a formula. We were so amazed at his genius work that probably only Dr. Eviatar and Bench can understand it, because I know I didn't. Mr. K says, "If you don't understand something in class, you can bet that six other people in that class probably didn't get it as well." So I'm counting on other people to fill in the blanks that I've left in this blog post. Also, the formula that Bench gave us is something to be taught some time in the future. Anyways, we ended up getting the formula, y = nx^(n-1).
Derive f(x) = x^3.

Derive y = -1/x.
 Using the y = nx^(n-1) formula,
Using the y = nx^(n-1) formula,y = nx^(n-1)
y = (-1)x^[(-1)-1]
y = -x^-2
y = -1/x^2
END NOTES:
- Homework: 2.3 The Derivative Function #1, 5, 7, 9, 11, 12, 21, 27
- Note: The principal says we won't get our laptops until he talks to Mr. K (assuming that Mr. K gets back in action at our school). Well, guess what? WE ARE THE RADICAL CALCULUS GROUP. WE WANT OUR LAPTOPS, AND WE WANT OUR LAPTOPS NOW!
- Next scribe is Joyce.
Wednesday, October 1, 2008
Differentiables
*Truthiness may vary
Anyway, onto actual Mathematics, those darn derivative deriving derivates and what in the heck a differentiable function is. I cannot however tell you with absolute certainty what a differential is, but I have a good idea we're going to find out soon enough.
The basic definition of a differentiable is a function where the derivative can be found for any point of a defined segment of that function.
Which is why f(x) = x^2 is differentiable, because we can find the derivative for every point in the function or any portion of the function.
If you get a function with "kinks" or very pointy points when you graph it, it won't have derivatives at those pointy points and thus is not differentiable for the entire function.
However, if you define a segment of that function that doesn't have pointy points then you can say that the function is differentiable for this segment of the function.
The teacher's definition is as follows:
"A function (fcn) is said to be differentiable at variable a if at variable a f '(a) exists. It is called differentiable on an interval if it is differentiable for every number in the interval."
Here's the example from yesterday that we did today [Ex 1] (which we also did yesterday), and another example we did [Ex 2]. Both of these are differentiable, because the derivative f '(x) exists at x = 0. (in Example 1 replace variable a with x)
Ex 1)

(Click to view larger)
Ex 2)

(Click to view larger)
This is an example where f '(0) doesn't exist, therefore it is not differentiable.
Ex 3)

(Click to view larger)
As shown in the image, the function f(x) = |x| is not differentiable because when x = 0, its derivative does not exist/cannot be determined tangentially. If graphed, y = |x| would show it has a "kink" or pointy point at x=0.
At the end of class we started talking about the different people who invented Calculus, and importantly Joseph Louis Lagrange's contribution of f '(x) = dy/dx, which will come up later in the course I'm sure of it, because of this Wikipedia article.
The next scribe shall be...
Zeff (zeph)
Sorry this post is uncredibly late, you can blame Wired and NeoGAF for their unfairly up-to-date news. I started working on this post at 9pm and finished 4 hours later. Of course atleast one of those hours was spent trying to figure out OpenOffice...
