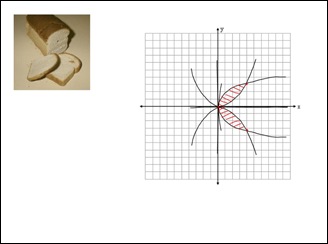
Here they are ...
Thursday, February 26, 2009
Java applet on solids of revolution
The Applied Math people are writing a quiz, so as promised, here is an applet that should help make things clearer.
Java applet on solids of revolution
I know there are a bunch of videos on this on YouTube as well. I'll see what I can find. Sorry for the confusion this morning.
Java applet on solids of revolution
I know there are a bunch of videos on this on YouTube as well. I'll see what I can find. Sorry for the confusion this morning.
The nearly forgotten blog post: Solids
Hey guise, its *squeak* Not Paul here, blogging about our class.
The nearly forgotten part is because its like 1AM and I was about to call it a night when I booted up my browser to check my email. What pops up? The blog. And I'm like, where's the scribe?
OH RIGHT!
So yeah, here we go again.
Today we worked on the stuff we sort of got introduced to yesterday, which was Solids. How do you find the area between two functions?! THATS CRAZY MAN.
In reality, it ain't so crazy, man. thinking about it logically, the integral can be found by integrating over the interval that ranges from the first intercept of the two functions to the second intercept (they NEED to have two intercepts, oth
erwise it'd go on forever).
I think this slide describes better what I'm tryin
g to say. Because me English so good not as much.

[Click pics for a larger version]
What's going on here is that we have two functions: f(x) and g(x). f(x) is equal to root x and g(x) is equal to x squared. Our mission, should we choose to accept it, is to find the area between the two functions. To do this, first we find the intercepts. The first one we know is zero, just by looking at the graph/sketch, or by simple reasoning. The second one can be found by using the equation f(x) = g(x) and solving for the variable (in this case x). This is because we want to find the value where f(x) and g(x) are equal. Doing this yields us the value 1 for the second intercept. Yay!
Now, we create an equation to find the area. Subtract one integral from the other, but both must be on the same interval (intercept 1 to intercept 2). Antidifferentiate, solve with fundamental theorem of calculus! Bada bing.
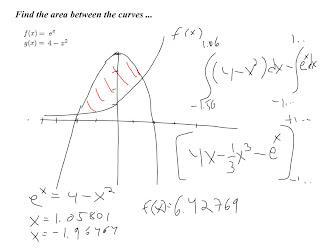
Now we move onto something a little trickier. Our first function, f(x), is e to the power x. Funny how that little guy seems to pop up everywhere. The second function, g(x), is 4 minus x squared.
Now, I said a little trickier, but really, is it any harder? No! The only difference is it might take a little longer due to anti differentiation, but longer is not equal to harder! You can even speed things up by graphing and using your graphing calculator to find the intercepts. Do a little antidifferentiation... algebra, and you're done before you know it.
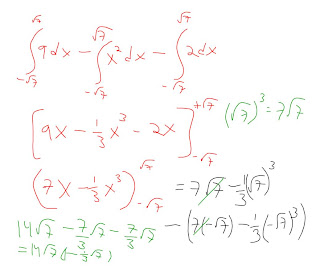
Eaaaaaaaaasy.
Bread: designed to make us hungry. *eats toast*
But, also a cool reminder that in math that it’s okay to approximate just a little. I mean, nothing is really truly exact. So what if that slice of bread really has that little bit of z axis breadth (pun intended)? Treat it like a 2 dimensional object, relatively, its no big deal.
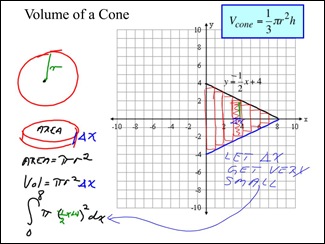
Now here’s when we get into the good stuff. Like shapes. Here, we use the circle area equation to find the integral of this cone. However, the cone is mapped to a 2D plane, so you cant really see all of it, but rest assured, its a cone. Now, see, this cone has the property that its radius at a certain height can be found using the equation r = –(1/2)x + 4. Do we really need any more information? We have the interval to integrate from (0 to 8, because the height is 8), and the function to integrate (area). Solution in the next slide:
And finally, a general rule to guide us. This should come in handy…
And with that, Im am done and tired, and in desperate need of some sleeeeeep.
Next scribe is the one and only Kristina.
Night guys.
Wednesday, February 25, 2009
Slides February 25th
Labels:
Applications of Integrals,
Dr. Eviatar,
Slides
Slides February 24th
Labels:
Applications of Integrals,
Dr. Eviatar,
Slides
Tuesday, February 24, 2009
Working with the Absolute Values
Hello everyone,
My name is Ben and I'll be your scribe for today.
We started off with a very awkward question. We were asked to find the displacement of a car driving East or West from a certain place, but the question itself was unsolvable (is that a word? Anyways,). We saw that it was unsolvable because we weren't given a function or some sort of thing to represent the changes in velocity over the trip. The car could have been moving in one direction and back the same distance or it could have been moving in only one direction.
Then the next slide gave us our velocity function to find the displacement. We just used basic integration and found the displacement. Notice that we can actually find out where the object was. Normally if you were to integrate a velocity function you would only have a change in position with no exact location. We were given a reference point or a starting point so we can find out where it was after the given amount of time.
The next few slides involved the same type of work. Integrate the function to find the change in position or displacement.
Then we were asked to find the total distance of an object's travels. Note that we were supposed to find the DISTANCE. To find the distance we integrate the absolute value of the function.
The next slide was a generalization or a "What did we learn today" slide. Technically we didn't learn anything new because we already did it in chapter 6 I believe but it was a refresher.
If you integrate a velocity function you will find a change in position, it can be negative or positive or even zero depending on the direction of movement. If we were to integrate the absolute value of the velocity function we would get the total distance. If you were to take the absolute value of the integration of the velocity function you just get the change in position but it will be positive. I'm not sure if there is a use for that type of technique but I hope we talk about it tomorrow.
Homework is Chapter 18.1 Exercises 1-15 odd. The next scribe will be Paul which is not Not Paul but Francis, but by Francis I mean Not Paul.....................
My name is Ben and I'll be your scribe for today.
We started off with a very awkward question. We were asked to find the displacement of a car driving East or West from a certain place, but the question itself was unsolvable (is that a word? Anyways,). We saw that it was unsolvable because we weren't given a function or some sort of thing to represent the changes in velocity over the trip. The car could have been moving in one direction and back the same distance or it could have been moving in only one direction.
Then the next slide gave us our velocity function to find the displacement. We just used basic integration and found the displacement. Notice that we can actually find out where the object was. Normally if you were to integrate a velocity function you would only have a change in position with no exact location. We were given a reference point or a starting point so we can find out where it was after the given amount of time.
The next few slides involved the same type of work. Integrate the function to find the change in position or displacement.
Then we were asked to find the total distance of an object's travels. Note that we were supposed to find the DISTANCE. To find the distance we integrate the absolute value of the function.
The next slide was a generalization or a "What did we learn today" slide. Technically we didn't learn anything new because we already did it in chapter 6 I believe but it was a refresher.
If you integrate a velocity function you will find a change in position, it can be negative or positive or even zero depending on the direction of movement. If we were to integrate the absolute value of the velocity function we would get the total distance. If you were to take the absolute value of the integration of the velocity function you just get the change in position but it will be positive. I'm not sure if there is a use for that type of technique but I hope we talk about it tomorrow.
Homework is Chapter 18.1 Exercises 1-15 odd. The next scribe will be Paul which is not Not Paul but Francis, but by Francis I mean Not Paul.....................
Labels:
Applications of Integrals,
benofschool,
Scribe Post
Monday, February 23, 2009
Post Antiderivatives Test
Another test over with. Was it me or was that test extremely long? I barely had enough time to finish it. I completed all of the long answers (1st one was a doozy). The multiple choice took the longest overall because there was like 4 pages of them. But I was well prepared for the types of questions. I wasn't expecting that long of a test.
Enough about me. How about everyone else? How did you think you did on the test? What were the hard parts? Easy Parts?
Enough about me. How about everyone else? How did you think you did on the test? What were the hard parts? Easy Parts?
Sunday, February 22, 2009
Chapter 8.1
Friday's class was supposed to be test day but plans change. No worries though, no time was wasted. We immediately started chapter 8.1. The class went through the chapter on that site mr. k said to go on. He was also right about the chapter being not so difficult. It was all about antidifferentiating velocity.
The only new stuff was total distance traveled. Our math book gave a good explanation of this. For example, if you take 5 steps forward and 3 steps back the net change would be 2, however the total change would be 8! So we learned to find total change we'd need to use absolute value sign. We also have to find the interval where the velocity is positive and negative and antidifferentiate them. We then add those them together to find the total distance.
Yes...that is my scribe post. Next scribe will be benchi-man. I'm not really sure what to tag this as...........
The only new stuff was total distance traveled. Our math book gave a good explanation of this. For example, if you take 5 steps forward and 3 steps back the net change would be 2, however the total change would be 8! So we learned to find total change we'd need to use absolute value sign. We also have to find the interval where the velocity is positive and negative and antidifferentiate them. We then add those them together to find the total distance.
Yes...that is my scribe post. Next scribe will be benchi-man. I'm not really sure what to tag this as...........
Friday, February 20, 2009
BOBBing
Hi Everyone,
Unfortunately I am going to miss the test because I am attending S.E.T 2009 at U of M. I was given permission to write the test on Monday during my spare.
This unit was quite fun because I got to play around with equations like in grade 12 Pre-Calculus in the Logarithm and Trig Identities unit. The hardest integrals to evaluate were the inverse trigonometic functions like arctan and arcsin because when they appear in a question, you have to write it in a way that fits the actual derivative or antiderivative. But with a little time and clever factoring the question can be solved.
The most useful thing that I learned in this unit was the substitution technique where we had to substitute a function as a variable. It was very funny how Mr K explained how to use the technique because it always sounded like some sort of motivational speaking. Jamie knows what I'm talking about.
That is my BOB for the Antiderivatives unit. Sorry Mr.K for not informing you about my absence earlier but I informed Dr. Eviatar. Hopefully you are okay with that Mr. K.
Good Night and wish me luck on Monday :D
Unfortunately I am going to miss the test because I am attending S.E.T 2009 at U of M. I was given permission to write the test on Monday during my spare.
This unit was quite fun because I got to play around with equations like in grade 12 Pre-Calculus in the Logarithm and Trig Identities unit. The hardest integrals to evaluate were the inverse trigonometic functions like arctan and arcsin because when they appear in a question, you have to write it in a way that fits the actual derivative or antiderivative. But with a little time and clever factoring the question can be solved.
The most useful thing that I learned in this unit was the substitution technique where we had to substitute a function as a variable. It was very funny how Mr K explained how to use the technique because it always sounded like some sort of motivational speaking. Jamie knows what I'm talking about.
That is my BOB for the Antiderivatives unit. Sorry Mr.K for not informing you about my absence earlier but I informed Dr. Eviatar. Hopefully you are okay with that Mr. K.
Good Night and wish me luck on Monday :D
BOBbing for Calculuses: Antiderivatives Edition
So yeah, test tomorrow (or today if you wanna get technical). What's it about? Antidifferentiation!
Woo. Hoo.
I thing is, when we were going through the course, I feel like I understood what was going on, but now I don't really think I understand it as much after all. The integrals stuff was definitely my least favourite stuff, and some of the antidifferentiation rules and techniques were a little hazy on me. Specifically, substitution. Arc trig stuff was fairly simple and straightforward though.
However, the recent stuff I feel good with. Perhaps all this can be clarified by a bit of note reading.
Thursday, February 19, 2009
BOB: Chapter 7
Hello everyone. Is everyone ready for the test?! I think I am... Anyways, I liked this chapter a whole lot more than the last few. Finding anti derivatives using substitution and integration by parts was hard at first but after more practice and help from those spare days, I think I got them down, for the most part. Though I still have problems finding out how to rearrange the function so that my "du" can fit into it when doing substitution. That's the most tricky part indeed. I will also need to remember my "+ C"s for sure, but after having done some more practice on anti differentiation, I'm sure I won't forget about them this time... I hope.
Yep, the midpoint, trapezoid, and error stuff seem to be okay. But we'll see if I really understand them on the test.
Okay, good luck on the test everyone!
Yep, the midpoint, trapezoid, and error stuff seem to be okay. But we'll see if I really understand them on the test.
Okay, good luck on the test everyone!
BOB Version 7: Finding Antiderivatives
I thought this unit easier than the previous unit because it's mechanical, but I was surprised on what I got on the antiderivative quiz. Substitution and integration by parts now makes sense to me, although antidifferentiating arctrig functions isn't second nature to me as of yet. I hope I'll meet the expectation of having these skills "fluid" by the time I write the test. It's also my hope that I can solve problems like the ones we had on our pretest without the use of a calculator, but using the calculator isn't time-consuming, if you understand, but, just like the pretest, I predict there will be one question on the test in the open response that will be challenging to answer. I hope I'm prepared for that when the time comes.
Guess who's back? BOB
Today in class we had a pretty simple and straight forward pre-test. It was 4 mulitple choice and 1 free response. The pre-test questions ranged from definite integrals, such as finding the area under a graph in a certain interval, to integration by parts and substitution to find the antiderivative of a certain functions.
For question 1 of multiple choice I used the rsum program on my calculator to find the actual value of the function through the interval [1,3] and then I found the area under the graph on the interval [1,3] and there was a difference of 0.0416667 which is approximately 1/24, which was anwser B.
For question 2 I used trial and error on my calculator finding the area under the curve of the graph. Whichever equaled 6, would be the correct anwser, which was option D.
Question 3 was also the same concept as question 2. Where ln2 was equal to approximately 0.693, and I used trial and error to find the area under the curve that equaled ln2.
Question 4 was easily solved, just use integration by parts on the function y = xcos(x) and you should end up with option A.
Open response was a bit harder but not by much. For part a) we used substituion to find the antiderivative and then we found what it would equal at each endpoint and the table made it easy by giving us the values. Part b) was the same deal, but we used integration by parts.
Overall this pre-test was by far the easiest, in my perspective. Good luck everyone. It's time to BOB.
I was never really worried about this unit, because all of it seemed really straight forward. I was really only worried about when to use what, such as substitution and integration by parts to find an antiderivative. I know I won't have trouble solving either of them, as long as I make the right decision in the first place. The midpoint sum, trapezoid sum and Simpson sum seem to be quite easy, but I do believe we could have spent maybe a class or two more in this section. I didn't see these type of questions in the pre-test so this is maybe why it seemed brief in class, because it won't be a significant part in the test. I feel quite comfortable going into the test, as long as we're allowed to use our calculators. I'd be nothing without the graph and rsum programs!
The next scribe will be! Joyce.
For question 1 of multiple choice I used the rsum program on my calculator to find the actual value of the function through the interval [1,3] and then I found the area under the graph on the interval [1,3] and there was a difference of 0.0416667 which is approximately 1/24, which was anwser B.
For question 2 I used trial and error on my calculator finding the area under the curve of the graph. Whichever equaled 6, would be the correct anwser, which was option D.
Question 3 was also the same concept as question 2. Where ln2 was equal to approximately 0.693, and I used trial and error to find the area under the curve that equaled ln2.
Question 4 was easily solved, just use integration by parts on the function y = xcos(x) and you should end up with option A.
Open response was a bit harder but not by much. For part a) we used substituion to find the antiderivative and then we found what it would equal at each endpoint and the table made it easy by giving us the values. Part b) was the same deal, but we used integration by parts.
Overall this pre-test was by far the easiest, in my perspective. Good luck everyone. It's time to BOB.
I was never really worried about this unit, because all of it seemed really straight forward. I was really only worried about when to use what, such as substitution and integration by parts to find an antiderivative. I know I won't have trouble solving either of them, as long as I make the right decision in the first place. The midpoint sum, trapezoid sum and Simpson sum seem to be quite easy, but I do believe we could have spent maybe a class or two more in this section. I didn't see these type of questions in the pre-test so this is maybe why it seemed brief in class, because it won't be a significant part in the test. I feel quite comfortable going into the test, as long as we're allowed to use our calculators. I'd be nothing without the graph and rsum programs!
The next scribe will be! Joyce.
BOB The Antideriver
Well this is my umpteenth BOBbing. From what I recall, we started the method of substitution before break and I was so confident with it. Then there were the consequences of after break. Forgetting everything and not working hard enough.
Then integration by parts came in. I like this method, especially if the acronym LIATE is used to find out which value goes where.
But the thing I might have trouble with is, well the error formulas, because I wasn't here that day and using both integration by parts and substitution together. I still get confused. I had a little bit of trouble with the pretest today, but I understand it now. The thing I still can't really do is reversing some of the differentiation rules without consuming a lot of time, or..the ones I can barely do at all, such as "reversing the chain rule". Hopefully clear enough to do well on this test. I don't think I can afford another...well... downer.
But yes, good luck everyone, and I have to say, I quite enjoyed this unit of antidifferentiation.
Then integration by parts came in. I like this method, especially if the acronym LIATE is used to find out which value goes where.
But the thing I might have trouble with is, well the error formulas, because I wasn't here that day and using both integration by parts and substitution together. I still get confused. I had a little bit of trouble with the pretest today, but I understand it now. The thing I still can't really do is reversing some of the differentiation rules without consuming a lot of time, or..the ones I can barely do at all, such as "reversing the chain rule". Hopefully clear enough to do well on this test. I don't think I can afford another...well... downer.
But yes, good luck everyone, and I have to say, I quite enjoyed this unit of antidifferentiation.
Quick BOB!
K so the night before the test I find myself really irritated that I've been slacking off this chapter. After I looked through the slides, I realized that I was having trouble identifying which method (substitution or by parts) to use to antiderive. Solving the question is so much easier when you know which one to use. I especially need to work on all the mechanical stuff that Mr. K talked about before also. That's my bob for this unit...time to study.
Chapter 7 BOB
I liked this chapter, kinda. There's never gonna be a chapter that I absolutely like without problems. However I was relatively comfortable with the unit with the techniques of antidifferentiation like substitution and integration by parts. The only real problem is having to recognize which one to use.
Next was the Midpoint and Trapezoid sums were pretty straight forward. I think this test will be okay, but a hard okay. Lol.
Next was the Midpoint and Trapezoid sums were pretty straight forward. I think this test will be okay, but a hard okay. Lol.
bob
Bobs, antiderivatives, and integrals oh my!
So this is my bob post for this unit. How did this unit make me feel? well for the most part I definitely understood more of it then just about any unit we've done so far, the mechanical aspects of it make it appealing to me on so many levels ;p The substitution stuff was interesting, I found that to probably be some of the easier stuff, along with the anti-derivatives of the arc-trig functions.
The harder stuff would mostly be everything I wasn't in class to learn haha (Namely, integration by parts, and the stuff from tuesday) although it wasn't really all that bad. Overall I can safely say that I enjoyed this unit.
So I think thats everything, I'm off to do a bit of last minute studying before I hit the z's.
Night, and good luck everyone :]
The harder stuff would mostly be everything I wasn't in class to learn haha (Namely, integration by parts, and the stuff from tuesday) although it wasn't really all that bad. Overall I can safely say that I enjoyed this unit.
So I think thats everything, I'm off to do a bit of last minute studying before I hit the z's.
Night, and good luck everyone :]
Tuesday, February 17, 2009
Bad News Bears: Mr.K as - The Rock 'n Rolla
Today, we have received some news. Some serious news. As those who were in class, already know, but Mr. Kuropatwa will be gone next week for about 9 days. He will be gone for reasons I will not say, for they are very personal. We are all praying and wishing him the best.
Due to these events, Dr. Eviatar will return to substitute for 3 lessons of Chapter 8. Mr. K also gave us tinyurl's to assist us during that week should we have any concerns or confusions. I will post the tinyurl's now.
http://tinyurl.com/b94cgo - Chapter 8.1
http://tinyurl.com/c5c2nm - Chapter 8.2 & 8.3
All of them are interactive lessons. When he returns, we should be finishing up Chapter 8.3 or starting Chapter 8.4
Oh yeah, we have a test on Friday, be there or be cubed!
Starting off our 'Spare Lesson', we reviewed the Left and Right hand sums. After that we reviewed the midpoint and trapezoid sums. (I find it that I shouldn't have to really explain it here as it is explained in detail in the scribe post below)
Now after doing the homework that Mr. K assigned us, we found that the Midpoint errors were approximately half of that of a Trapezoid sum, therefore Midpoint sums are more accurate by approximately double that of a Trapezoid sum.
Error Estimates for Trapezoid & Midpoint Sums

So to use this, we 'choose' the accuracy then find n, so we know how many rectangles there are.
The Simpson Sum

No, Not Homer Simpson. The next sum was made by a mathematician who found a way to combine the two sums. He tried it in a different way, he tried to calculate using little parabolas.
 So for example, we'll use M4 and T4, because if you have both, you can find a Simpson Sum.
So for example, we'll use M4 and T4, because if you have both, you can find a Simpson Sum.
M4 = 0.2422
T4 = 0.2656
So just plug it in and...

 to within an error of 0.001 using a:
to within an error of 0.001 using a:
a)trapezoidal sum - How many intervals, n, are required?
b)How many intervals are required using a midpoint sum?
Wow, did that honestly take me two hours? Geeez ¬__¬" Anyways, I still have loads of homework to do, so I'm gonna go do that and stay up for a few hours. Expect me to be either grumpy or tired so yeah :D. Oh yeah, next scribe will be Francis.
Also I thought I'd bring this to everyone's attention.
Take the Vow
Over one billion children live in poverty. Hunger is only one of their challenges; exploitation, abuse and discrimination haunt them on a daily basis. Many live in remote areas of the world and have little, or no, education.
They have no rights. They have no voice.
On March 5, 2009, people around the world will remain silent for 24 hours in support of those who are unable to speak up themselves.
Join the quiet revolution.
Take the Vow of Silence.
Go to I am Silent for more information.




Due to these events, Dr. Eviatar will return to substitute for 3 lessons of Chapter 8. Mr. K also gave us tinyurl's to assist us during that week should we have any concerns or confusions. I will post the tinyurl's now.
http://tinyurl.com/b94cgo - Chapter 8.1
http://tinyurl.com/c5c2nm - Chapter 8.2 & 8.3
All of them are interactive lessons. When he returns, we should be finishing up Chapter 8.3 or starting Chapter 8.4
Oh yeah, we have a test on Friday, be there or be cubed!
Starting off our 'Spare Lesson', we reviewed the Left and Right hand sums. After that we reviewed the midpoint and trapezoid sums. (I find it that I shouldn't have to really explain it here as it is explained in detail in the scribe post below)
Now after doing the homework that Mr. K assigned us, we found that the Midpoint errors were approximately half of that of a Trapezoid sum, therefore Midpoint sums are more accurate by approximately double that of a Trapezoid sum.
Error Estimates for Trapezoid & Midpoint Sums
The Equation for Trapezoidal Sums

The Equation for Midpoint Sums
For the Midpoint sum equation, it's 24n^2 because it is more accurate.So to use this, we 'choose' the accuracy then find n, so we know how many rectangles there are.
The Simpson Sum

No, Not Homer Simpson. The next sum was made by a mathematician who found a way to combine the two sums. He tried it in a different way, he tried to calculate using little parabolas.
M4 = 0.2422
T4 = 0.2656
So just plug it in and...

((2(0.2422)) + (0.2656)) / 3 = 0.25
0.25 is the exact point of the integral we were using, but even though it was exact in this case, we'll call it an exact approximation. This tells us that the Simpson Sum is even more accurate than both sums.Approximate
 to within an error of 0.001 using a:
to within an error of 0.001 using a:a)trapezoidal sum - How many intervals, n, are required?
b)How many intervals are required using a midpoint sum?
A)
B)
f"(x) = 6x^-4, so max of f" on [1,2] occurs at 1.
f"(1) = 6, therefore M2 = 6
f"(1) = 6, therefore M2 = 6
0.001 = 1/(2n^2)
500 = n^2
22.3607 = n
From here, we round up because it can't be less than the error that we wanted. Less Intervals = Less Accuracy. So, n = 23.500 = n^2
22.3607 = n
B)
Wow, did that honestly take me two hours? Geeez ¬__¬" Anyways, I still have loads of homework to do, so I'm gonna go do that and stay up for a few hours. Expect me to be either grumpy or tired so yeah :D. Oh yeah, next scribe will be Francis.
Also I thought I'd bring this to everyone's attention.
Take the Vow
Over one billion children live in poverty. Hunger is only one of their challenges; exploitation, abuse and discrimination haunt them on a daily basis. Many live in remote areas of the world and have little, or no, education.
They have no rights. They have no voice.
On March 5, 2009, people around the world will remain silent for 24 hours in support of those who are unable to speak up themselves.
Join the quiet revolution.
Take the Vow of Silence.
Go to I am Silent for more information.




Monday, February 16, 2009
FRIDAY THE 13th indeed ♫ ♪ CARRY ON MY WAYWARD POST ♪ ♫
I apologize for the REALLY late scribe post. I'm not going to make excuses, or well, I'll try not to, but I'm just going to say... I felt like my brain died over this weekend. I only utilized Sunday and Monday for homework, as for those two days I could have used... well that was Valentines Day and I took some of that time just re-watching both versions of My Bloody Valentine and Friday....was.. well, need I say more? Friday The 13th. I don't recommend it...you know what Hollywood does to movies these days. They just sort of knock it down a couple notches when it comes to raw storytelling. But that's enough for now.
All that matters now is that I carry on. I'm in the mode right now and I'm ready to go. I've got my typing hands ready for blast off and I've got my 80's rock playlist already going. Don't ask why...for some people it's classical music that helps them concentrate, me, it's classic rock. CURRENT SONG: Carry On My Wayward Son - Kansas. oh Kansas... classic.... rock.... hit--- and the perfect song to keep you motivated, which is what we need lately in this class.From what I recall, we started Friday's class off with a little quiz. Or... it should have been little, based on what we've been learning lately. It's getting tense...and I still sense that we're behind. Really behind. We need to pick up the pace. Like Mr. K said, we can't keep continuing this way. Most of these things should be engraved in our head, and we should be able to get past this basic calculus. It should be "general knowledge" in a math sense. We're lagging behind, and that's not good. Because like he said, most of the stuff we're stumbling upon right now is assumed that we can do it by the time the AP exam comes along, and that's not very far. I know I'm one to talk [ha] but I think giving this little motivation kick in the noggin is necessary. Just a bit.
On to the quiz. I'm sure that I don't have to explain this too much, but I'll summarize it, and go over the most common mistakes that the majority of the class made. It's the least I can do for a scribe post like this.
 For this first question, integration by parts is used. Two issues some people might have is assigning the values to the right variable correctly and also, the general formula of integration by parts, which is the sequence we should multiply by in order to integrate the function correctly.
For this first question, integration by parts is used. Two issues some people might have is assigning the values to the right variable correctly and also, the general formula of integration by parts, which is the sequence we should multiply by in order to integrate the function correctly.
To determine which value goes where, we use the.......the....thing we learned. LIATE.; which stands for, Logarithmic, Inverse Trigonometric, Algebraic, Trigonometric. zomg.. I got it now. Acronym. Right? To determine which function is " g' ", g' must be the most complicated function in which it can be antidifferentiated. In this case, g' = sin t.
That being said, ---------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------


This was the second question on the quiz, but we saved this one for last, since it was the hardest, or perhaps longest to antidifferentiate. This one was a special case where both substitution and integration by parts was used. The first thing we did was substitute and put it in terms of u, but we still wound up with z's, so we couldn't go far with that. With that dead end, this is where integration by parts comes in, of course using the same structure as the previous question. Once it is antidifferentiated in the sense of u, we resubstitute back in the values for u and put it back in terms of z. ONCE AGAIN, "+ C"!!!
 There's a recurring phrase we use many-a-times in class; "There are many ways to skin a cat." Then of course, we always remember to mention the "PETA issue" regarding the actual skinning of a cat. This question, I think, can be done by either or, substitution or integration by parts. I think. Was this the question? I think. But from what I recall when I tried, I think it got messy using integration by parts. So we used substitution for this question. I think most of us got to the right answer for this one.
There's a recurring phrase we use many-a-times in class; "There are many ways to skin a cat." Then of course, we always remember to mention the "PETA issue" regarding the actual skinning of a cat. This question, I think, can be done by either or, substitution or integration by parts. I think. Was this the question? I think. But from what I recall when I tried, I think it got messy using integration by parts. So we used substitution for this question. I think most of us got to the right answer for this one. Then there was this question that came before the last one, but I just got mixed up with the printscreen capture order. Haha. My bad. I never got that saying. that's just like saying "I own bad as if it were a conceivable object, yet I'm using the phrase while bashing it. But this question, if I guess, the fundamentals of integration by parts are engraved in your head, this should be no biggie.
Then there was this question that came before the last one, but I just got mixed up with the printscreen capture order. Haha. My bad. I never got that saying. that's just like saying "I own bad as if it were a conceivable object, yet I'm using the phrase while bashing it. But this question, if I guess, the fundamentals of integration by parts are engraved in your head, this should be no biggie.
As for the rest of the class, we picked up where we left off and reviewed with examples, antidifferentiating combining the rules of integration of trig functions with other rules of integration.
Then we whipped our way back into using approximations when trying to find integrals when we can't exactly determine the antiderivatives.
The class took a look at monotonic functions and how to find the areas under the curve. We compared the methods to see which was more accurate and we found out that:
But the reason why these conditions work the way depends on these main points:
Once again... Carry On...My Wayward Son. [or just.. classmates.]
All that matters now is that I carry on. I'm in the mode right now and I'm ready to go. I've got my typing hands ready for blast off and I've got my 80's rock playlist already going. Don't ask why...for some people it's classical music that helps them concentrate, me, it's classic rock. CURRENT SONG: Carry On My Wayward Son - Kansas. oh Kansas... classic.... rock.... hit--- and the perfect song to keep you motivated, which is what we need lately in this class.From what I recall, we started Friday's class off with a little quiz. Or... it should have been little, based on what we've been learning lately. It's getting tense...and I still sense that we're behind. Really behind. We need to pick up the pace. Like Mr. K said, we can't keep continuing this way. Most of these things should be engraved in our head, and we should be able to get past this basic calculus. It should be "general knowledge" in a math sense. We're lagging behind, and that's not good. Because like he said, most of the stuff we're stumbling upon right now is assumed that we can do it by the time the AP exam comes along, and that's not very far. I know I'm one to talk [ha] but I think giving this little motivation kick in the noggin is necessary. Just a bit.
On to the quiz. I'm sure that I don't have to explain this too much, but I'll summarize it, and go over the most common mistakes that the majority of the class made. It's the least I can do for a scribe post like this.
 For this first question, integration by parts is used. Two issues some people might have is assigning the values to the right variable correctly and also, the general formula of integration by parts, which is the sequence we should multiply by in order to integrate the function correctly.
For this first question, integration by parts is used. Two issues some people might have is assigning the values to the right variable correctly and also, the general formula of integration by parts, which is the sequence we should multiply by in order to integrate the function correctly.To determine which value goes where, we use the.......the....thing we learned. LIATE.; which stands for, Logarithmic, Inverse Trigonometric, Algebraic, Trigonometric. zomg.. I got it now. Acronym. Right? To determine which function is " g' ", g' must be the most complicated function in which it can be antidifferentiated. In this case, g' = sin t.
That being said,
 ---------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------

This was the second question on the quiz, but we saved this one for last, since it was the hardest, or perhaps longest to antidifferentiate. This one was a special case where both substitution and integration by parts was used. The first thing we did was substitute and put it in terms of u, but we still wound up with z's, so we couldn't go far with that. With that dead end, this is where integration by parts comes in, of course using the same structure as the previous question. Once it is antidifferentiated in the sense of u, we resubstitute back in the values for u and put it back in terms of z. ONCE AGAIN, "+ C"!!!
 There's a recurring phrase we use many-a-times in class; "There are many ways to skin a cat." Then of course, we always remember to mention the "PETA issue" regarding the actual skinning of a cat. This question, I think, can be done by either or, substitution or integration by parts. I think. Was this the question? I think. But from what I recall when I tried, I think it got messy using integration by parts. So we used substitution for this question. I think most of us got to the right answer for this one.
There's a recurring phrase we use many-a-times in class; "There are many ways to skin a cat." Then of course, we always remember to mention the "PETA issue" regarding the actual skinning of a cat. This question, I think, can be done by either or, substitution or integration by parts. I think. Was this the question? I think. But from what I recall when I tried, I think it got messy using integration by parts. So we used substitution for this question. I think most of us got to the right answer for this one. Then there was this question that came before the last one, but I just got mixed up with the printscreen capture order. Haha. My bad. I never got that saying. that's just like saying "I own bad as if it were a conceivable object, yet I'm using the phrase while bashing it. But this question, if I guess, the fundamentals of integration by parts are engraved in your head, this should be no biggie.
Then there was this question that came before the last one, but I just got mixed up with the printscreen capture order. Haha. My bad. I never got that saying. that's just like saying "I own bad as if it were a conceivable object, yet I'm using the phrase while bashing it. But this question, if I guess, the fundamentals of integration by parts are engraved in your head, this should be no biggie.As for the rest of the class, we picked up where we left off and reviewed with examples, antidifferentiating combining the rules of integration of trig functions with other rules of integration.
Then we whipped our way back into using approximations when trying to find integrals when we can't exactly determine the antiderivatives.
The class took a look at monotonic functions and how to find the areas under the curve. We compared the methods to see which was more accurate and we found out that:
- In MONOTONIC INCREASING fcns, taking the left hand sum is an underestimate and vice-versa, the right hand sum being an overestimate.
- In MONOTONIC DECREASING fcns, the left hand sum is an overestimate while the right hand sum is an underestimate.
But the reason why these conditions work the way depends on these main points:
- The TONICITY of the graph, how much of a curve there is, wide or steep, etc.
- Whether you take the LEFT or RIGHT sum.
- The CONCAVITY of the graph, whether it's concave up or concave down.
Once again... Carry On...My Wayward Son. [or just.. classmates.]
Labels:
.:. J + ME .:.,
Antiderivatives,
Scribe Post
Sunday, February 15, 2009
Found some cool stuff, Team PSY video
http://www.youtube.com/watch?v=NxJq60ZxFrw
Took so loooong
Anyway, guys, I also ran across some great stuff you may be interested in. MIT has an online site called OCW (Online Course Work), which uses Youtube to hold videos of course lectures. Im sure we could all use these for studies and to get a feel for University style study.
The main page is http://ocw.mit.edu, with the mathematics section being here:
http://ocw.mit.edu/OcwWeb/web/courses/av/index.htm#Mathematics
http://ocw.mit.edu/OcwWeb/web/courses/av/index.htm#Mathematics
They keep links to pages with the videos, and they're even avaliable to download so you can peruse them in your free offline time, or on your iPod! (neat)
Here's one page that has video links to stuff we've already learned. Good for brushing up.
I havent gone through much of it, but this site also seems to cover coursework and lectures for more advanced calculus, in case anybody is interested in seeing what we're doing next.
Also, NOT just Calc stuff there, MANY subjects covered. I personally will be looking into the computer science stuff they have, neat stuff.
Friday, February 13, 2009
Thursday, February 12, 2009
Omgosh fast scribelists and approximations.
Okay guys, I'm here again, scribing, which makes no sense to me cause like, I scribed only a few weeks ago it feels like. Anyways todays topic, beside omgosh lightning fast scribe posts, is Approximation, or more specifically, how approximate is approximate?
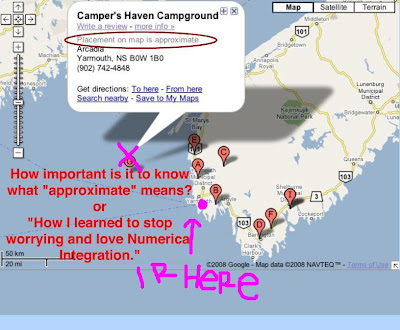
Now the real location of that campground is somewhere around the big purple dot and letters, NOT near the big purple x and the lies that google tells us. According to google, approximate locations means somewhere within about 40 miles which I can safely say is a bit much.
So the main thing to take away from this, was that when dealing with things as approximations you need to know how good the approximations are. Moving on.

You should recognize these as the questions homework from the other day. Mr. K kindly went through the solution of one lightning fast, while simultaneously commenting on how the other should also work out to be an arctan. The actual solution process shown there is somewhat straightforward. Bring the 100 out of the brackets so you get 1 + something, then make the x2/100 a square by turning it into (x/10)2. From there apply substitution, and voila. The second requires some completing the square to solve, nothing really too complicated, just good practice.
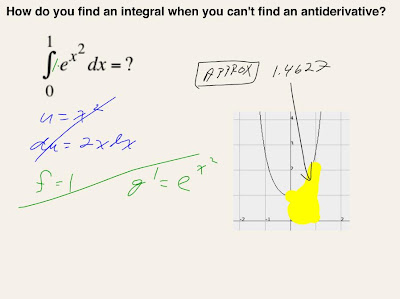
K so the next topic, is shown here on the slide. How do you find an integral when you can't find an anti derivative? On the slide you see us trying some methods we know to integrate ex2. We find substitution doesn’t work because, say you choose x squared as your u, you can get rid of the 2 once you find du but you cant get rid of the x. Also, integration by parts doesn’t work because your f’ is e to the x squared which we're trying to integrate in the first place, and conversely, don’t know the derivative of.
Here's some notes about the above slide that I took in class.
- e to the x squared is u shaped, but not a parabola. The parent function of this is similar to x cubed, but is not x cubed because things happen much faster. Everything is very abrupt.
- Finding the definite integral (I think?) of this function on your calculator gives an approx value of 1.4627
Next slide(s)!

Link: www.tinyurl.com/bu9kzs
Link: www.tinyurl.com/c4mwmo
link: www.tinyurl.com/Cojrp9
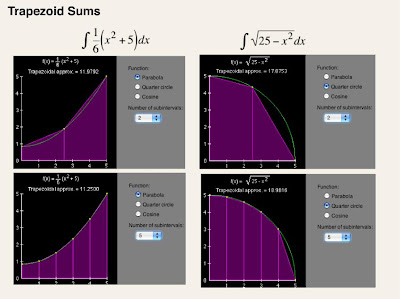
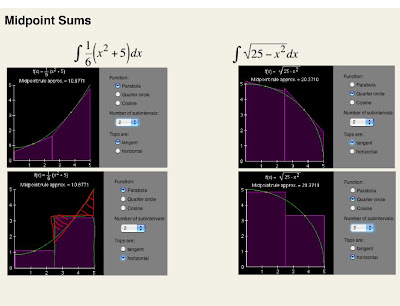
Okay, so all this might be a bit overwhelming, and confusing, but all we were really doing here, was comparing the accuracy of these various different approximation methods. As you can see, we compared normal old boring left and right hand sums, moderately exciting trapezoidal sums, and superb midpoint or tangent sums. Overall there were a couple main things to take away from the comparisons.
When trying to figure out if your estimate is and underestimate or an overestimate what it is depends on;
-The tonicity of the function
-If it is concave up or concave down
And
-If you are taking a right hand sum or a left hand sum.
But what’s the difference between a value of 3 and a value of 300?
-How concave the graph is.
And
The first derivative test deals with increase and decrease, while the second derivative test deals with concavity.
The main thing to take away from this scribe (and therefore this lesson) can be seen in this quote taken from a very knowledgeable person.
"When you do an approximation its important to say how approximate is approximate. Being off by 40 miles is not cool. In other words, you need to know how accurate it is. "
-Mr. K
Haha. I think he said that anyways. I might have translated it into my own words or something D:
J + Me Is gonna be the next scribe, and your homework is the homework from yesterday if you didnt do it, and the stuff on the last slide. To do the stuff with Trapezoid sums, use the riesum program on your calculator to figure out the right and left hand sums, then add those two, and divide by two. For the midpoint sum, Set your X Choice value in the Riesum program to .5 for the middle :]
Hopefully that wasnt too fast, and hopefully it all made sense.
Justus saying ciao, and goodnight.
:]
Now the real location of that campground is somewhere around the big purple dot and letters, NOT near the big purple x and the lies that google tells us. According to google, approximate locations means somewhere within about 40 miles which I can safely say is a bit much.
So the main thing to take away from this, was that when dealing with things as approximations you need to know how good the approximations are. Moving on.
You should recognize these as the questions homework from the other day. Mr. K kindly went through the solution of one lightning fast, while simultaneously commenting on how the other should also work out to be an arctan. The actual solution process shown there is somewhat straightforward. Bring the 100 out of the brackets so you get 1 + something, then make the x2/100 a square by turning it into (x/10)2. From there apply substitution, and voila. The second requires some completing the square to solve, nothing really too complicated, just good practice.
K so the next topic, is shown here on the slide. How do you find an integral when you can't find an anti derivative? On the slide you see us trying some methods we know to integrate ex2. We find substitution doesn’t work because, say you choose x squared as your u, you can get rid of the 2 once you find du but you cant get rid of the x. Also, integration by parts doesn’t work because your f’ is e to the x squared which we're trying to integrate in the first place, and conversely, don’t know the derivative of.
Here's some notes about the above slide that I took in class.
- e to the x squared is u shaped, but not a parabola. The parent function of this is similar to x cubed, but is not x cubed because things happen much faster. Everything is very abrupt.
- Finding the definite integral (I think?) of this function on your calculator gives an approx value of 1.4627
Next slide(s)!
Link: www.tinyurl.com/bu9kzs
Link: www.tinyurl.com/c4mwmo
link: www.tinyurl.com/Cojrp9
Okay, so all this might be a bit overwhelming, and confusing, but all we were really doing here, was comparing the accuracy of these various different approximation methods. As you can see, we compared normal old boring left and right hand sums, moderately exciting trapezoidal sums, and superb midpoint or tangent sums. Overall there were a couple main things to take away from the comparisons.
When trying to figure out if your estimate is and underestimate or an overestimate what it is depends on;
-The tonicity of the function
-If it is concave up or concave down
And
-If you are taking a right hand sum or a left hand sum.
But what’s the difference between a value of 3 and a value of 300?
-How concave the graph is.
And
The first derivative test deals with increase and decrease, while the second derivative test deals with concavity.
The main thing to take away from this scribe (and therefore this lesson) can be seen in this quote taken from a very knowledgeable person.
"When you do an approximation its important to say how approximate is approximate. Being off by 40 miles is not cool. In other words, you need to know how accurate it is. "
-Mr. K
Haha. I think he said that anyways. I might have translated it into my own words or something D:
J + Me Is gonna be the next scribe, and your homework is the homework from yesterday if you didnt do it, and the stuff on the last slide. To do the stuff with Trapezoid sums, use the riesum program on your calculator to figure out the right and left hand sums, then add those two, and divide by two. For the midpoint sum, Set your X Choice value in the Riesum program to .5 for the middle :]
Hopefully that wasnt too fast, and hopefully it all made sense.
Justus saying ciao, and goodnight.
:]
Wednesday, February 11, 2009
Antidifferentiating the Inverses of Trigonometric Functions
OVERVIEW:

Slide 2
These are the derivative and antiderivative rules that we discovered in the previous class.

Slide 3
The denominator with a square root! Factoring won't do us any good here (I've tried already) because we want the fraction to look similar to arcsinx, so we complete the square. *zeph thinks back to grade 11 precal*
AND VOILA! We were lucky. It looks very similar to the arctanx function when, using the method of substitution, we let u = x - 3 and find the derivative of u (du), and also because the denomiator has 1 - u as its radicand. (But what if that 1 was another constant? We'll look at that later, but for now, let's solve this problem first!) Using the antderivative rules, we know that the antiderivative of 1/sqrt(1-u^2) is arcsinu + C. Resubsituting u into arcsinu + C, we get the answer!

Slide 4
Now what if that 1-(x-3)^2 underneath the radicand was 5-(x-3)^2? There's no 5 in the derivative of arcsinx, so we put it there by doing a neat trick. In the green on the right side of the slide, we factored out a five, rewrote (x-3)^2/5 as ((x-3)/sqrt(5))^2 (since 5 = sqrt(5)^2), and rewrote (x-3)/sqrt(5) as x/sqrt(5) - 3/sqrt(5) in blue. We let the blue stuff equal u and differentiated it to du. Rewriting the expression in terms of u, we get 1/sqrt(1-u^2) which we can resubstitute u back in to get the answer.

Slide 5
To let the left-hand side equal the right-hand side, let's take the derivative of both sides since we're dealing with antiderivatives. Differentiating arcsin(x/a), via chain rule, and replacing the resulting denominator with an algebraic equivalent (look in box--we let the 1 = a^2/a^2 and factored out 1/a^2) to get 1/sqrt(a^2-x^2). Therefore, left-hand side equals right-hand side.
 Slide 6
Slide 6
For the left question, we used what we generalized in the box in slide 5 to "simplify" the denominator. Then we factored out a 1/10 using the constant multiple rule. Using the method of substitution, we let u = 3x/10, find its derivative (du), and rewrite the expression in terms of u. We realize that the antiderivative of the blue is arcsinu+C. We can then resubstitute u back into the expression to get the answer.
The middle and right questions we haven't done yet.
HOUSEKEEPING:
- Formulas for the derivatives and the antiderivatives of the inverses of the trigonometric functions
- Antidifferentiating the inverses of trigonometric functions using techniques such as completing the square, the chain rule, substitution, and multiplying by one and using the constant multiple rule
- Proving an antiderivative of a derivative is equal to the derivative of an antiderivative

Slide 2
These are the derivative and antiderivative rules that we discovered in the previous class.

Slide 3
The denominator with a square root! Factoring won't do us any good here (I've tried already) because we want the fraction to look similar to arcsinx, so we complete the square. *zeph thinks back to grade 11 precal*
AND VOILA! We were lucky. It looks very similar to the arctanx function when, using the method of substitution, we let u = x - 3 and find the derivative of u (du), and also because the denomiator has 1 - u as its radicand. (But what if that 1 was another constant? We'll look at that later, but for now, let's solve this problem first!) Using the antderivative rules, we know that the antiderivative of 1/sqrt(1-u^2) is arcsinu + C. Resubsituting u into arcsinu + C, we get the answer!

Slide 4
Now what if that 1-(x-3)^2 underneath the radicand was 5-(x-3)^2? There's no 5 in the derivative of arcsinx, so we put it there by doing a neat trick. In the green on the right side of the slide, we factored out a five, rewrote (x-3)^2/5 as ((x-3)/sqrt(5))^2 (since 5 = sqrt(5)^2), and rewrote (x-3)/sqrt(5) as x/sqrt(5) - 3/sqrt(5) in blue. We let the blue stuff equal u and differentiated it to du. Rewriting the expression in terms of u, we get 1/sqrt(1-u^2) which we can resubstitute u back in to get the answer.

Slide 5
To let the left-hand side equal the right-hand side, let's take the derivative of both sides since we're dealing with antiderivatives. Differentiating arcsin(x/a), via chain rule, and replacing the resulting denominator with an algebraic equivalent (look in box--we let the 1 = a^2/a^2 and factored out 1/a^2) to get 1/sqrt(a^2-x^2). Therefore, left-hand side equals right-hand side.
 Slide 6
Slide 6For the left question, we used what we generalized in the box in slide 5 to "simplify" the denominator. Then we factored out a 1/10 using the constant multiple rule. Using the method of substitution, we let u = 3x/10, find its derivative (du), and rewrite the expression in terms of u. We realize that the antiderivative of the blue is arcsinu+C. We can then resubstitute u back into the expression to get the answer.
The middle and right questions we haven't done yet.
HOUSEKEEPING:
- Breaking the chain, Hi I'm Justus, you're up next.
- Middle and right questions, do for homework, I assume.
- Today is Day 3 of the school day cycle. Today is an optional class.
- All calculus students will be writing the grade 12 contest on the 18th, which are able to win $1000, but .:. J + ME .:. and Hi I'm Justus may need to reschedule their plans for the DMCI Jr. High Tours on the 18th and 19th.
- You may achieve a high school credit for tutoring an EAL student in math for 100 hours.
- And don't forget to listen to the Dr. Love messages at the last ten minutes of class!
Tuesday, February 10, 2009
Finding the arctrig derivatives
OK, first scribe for this Semester^_^
We starts off with the graph of
arc sin

arc cos
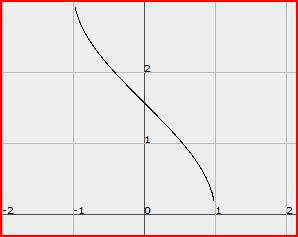
arc tan

Then we come up with the idea that arc sin and arc cos are similar, they have the same domains, they are just the inverse of each other.
Then it's time to find the derivative for arctrig:
1/ y=arc sin(x)
First let sin(y)=x sin(y)= x/1
then find the derivatives by using the chain rule 


there fore the derivative of arc sin is:

2/y=arc cos(x)
well these two are the similar steps so I will use Mr. K 's work

3/ y=arc tan(x)

~something really important Mr.K talked about in class.
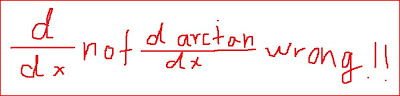
Every derivative rule have an anti-derivative rule:

then 2 more problem to solve:


Like Mr.K said we didn't learn a new technique to solve this type of problems. In these questions we used substitution and Integration by parts to find the anti-derivative.
Nothing much is new all we have to do is look for pattens.
Homework: ex7.5 odds and 24
next scribe is ................ Zeph
oh the chat box is there!!!
bye for now^_^
By the way Mr.K, the Chinese visitors of these 2 blogs is my friend in China that I tell her to check our blog out. ^_^ No surprising ^_^
We starts off with the graph of
arc sin
arc cos
arc tan
Then we come up with the idea that arc sin and arc cos are similar, they have the same domains, they are just the inverse of each other.
Then it's time to find the derivative for arctrig:
1/ y=arc sin(x)
First let sin(y)=x sin(y)= x/1
then find the derivatives by using the chain rule
there fore the derivative of arc sin is:
2/y=arc cos(x)
well these two are the similar steps so I will use Mr. K 's work
3/ y=arc tan(x)
~something really important Mr.K talked about in class.
Every derivative rule have an anti-derivative rule:
then 2 more problem to solve:
Like Mr.K said we didn't learn a new technique to solve this type of problems. In these questions we used substitution and Integration by parts to find the anti-derivative.
Nothing much is new all we have to do is look for pattens.
Homework: ex7.5 odds and 24
next scribe is ................ Zeph
oh the chat box is there!!!
bye for now^_^
By the way Mr.K, the Chinese visitors of these 2 blogs is my friend in China that I tell her to check our blog out. ^_^ No surprising ^_^
Subscribe to:
Posts (Atom)