
Welcome to 11.27.08's Calvin and Hobbes Themed Scribe Post!
*Post production thought* After posting this I noticed my images got cutoff because they weren't uploaded to blogger (since it takes 298372 years to upload one image, and I had 89723498 images to do, I decided to upload to the faster photobucket.) I'll have to upload most of them directly to the scribe post. However, I'll do that later ;p
*Post production edit* Okay guys, I think all the images are resized and fitted now. Remember, to see an image full size, all you gotta do it click it. Enjoy! :]
Hello there! This is Justus and I'll be doing the scribe for Thursday November 27th. I decided to make it Calvin and Hobbes themed, because,
1. I like Calvin and Hobbes, and...

2. Calvin's unique outlook on a lot of things seem to parallel with some of the opinions floating around our class at present.
Thus I thought it would be appropriate. Enjoy!
~Justus
*Note* All of the images were pulled off google, so I don't have direct source links for all of them. However, the Calvin and Hobbes characters, and comics are copyright Bill Waterson. I do not claim ownership to any of the images used, although I did edit some of them for the purpose of this blog (ex. The heading banner.)
Sorry if using these images is bad D: Anyways onward with these shenanigans!

At the beginning of the second period on November 27th, 2008 we came into class to see a lovely cubic type graph which Mr. K had drawn for us up on the not so smart board. Now, this is deceiving, because after our usual 10 minute opening banter, we did absolutely nothing with this graph and instead, went on to begin proofing three, of the differentiation rules we had learned while Dr. Eviatar was with us. Without any complaint from us, Mr. K began to take us back in time, to differentiation rules.

Differentiation Rules and Their Proofs
The derivative of a constant
For the constant function rule, we start with something looking like this
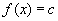
Where c is a constant (and therefore, f(x) is always c, no matter what x values are used. For example, f(2) = c, f(5) = , and f(2394273472934) also, = c.)
Applying the definition of a derivative (a derivative is the slope of a line tangent to the parent function) we easily see that;
If
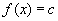
Then




This is because the graph of f(x) = c is horizontal. Since slope is (rise/run) a rise value of 0 gives you (0/run) which is always 0. Easy enough right?
Derivative Rules for a Line
This is where things might get to be slightly tricky for some. Just remember to take it one step at a time though, and it’ll make enough sense. Don’t get this confused with the rule however, the rule is easy to remember, it’s the proof that might be difficult.
So, because we are looking at the derivative of a line, we know that;

*note* according to Mr. K, using “m” for slope is archaic, and you probably won’t see it in university, instead it will be f(x) = ax + b. Due to this fact I will be using the later format for the rest of this scribe post.




So far its just simple algebra. Based on the definition of a derivative

we just found f(x + h) so we need only add it back in for the next step, instead of doing it all at once. This helps keep our thoughts together, and keep us organized. Continuing on.




Looking at these past four steps, you should see that we simply added in f(x+h) and f(x) based on the definition of a derivative, and canceled out everything we could. This gave us ah / h, which we all know reduces to a.
Therefore, the derivative of a line, is the slope of a line. This in itself makes sense if you look at the written definition of a derivative, “A derivative is the slope of a line tangent to the parent graph." If you have a straight line, then the tangent line will lie along the line, and therefore, share the same slope. See? It all comes together in the end.
Now, let’s take a short intermission, as this next one is a LONG one indeed.
...And We're Back :]
Derivatives of Powers



HALT!
Before we can continue, we must once again travel back in time, to gr.12 Where we did Binomial Theorem.

Remember pascals triangle?
Well this is it. Basically for those of us who haven’t learned this yet, pascals triangle is formed by starting with 1 (at the tip) and bringing that number down to the left and right. Then, what you do is add any number who are touching to the left or right, and bring the sum down. It is illustrated in this second image by the purple lines. Adding any two number in the fashion illustrated by the purple arrows gives you the number the points of the arrows meet up at.
http://pc40sw08.blogspot.com/2008/05/binomial-theorum-fibonacci-vitruvian.html (link to last years scribe post on binomial theorem)
Basically, in order to expand f(x+h) = (x+h)^n you need to use binomial theorem which looks something like this.

Or

So these are some of the various ways to apply binomial theorem to expand a binomial (say (x + 2) ^ 9)
Using this knowledge of the binomial theorem, we can figure out what

expands out to.

Now using these two (f(x) and f(x+h)), and putting them into our tried and true definition of what a derivative is;

We get

So looking at this, you should see that x^n and -x^n cancel. Thus we’re left with

Now as Mr. K would say, this is where the magic happens. By pulling the “h” out of the whole thing your left with;

The h’s then cancel, and you get

BUT WAIT!

We’re not done yet. Because the limit is

once you’ve removed the h in the denominator and numerator, all terms which are associated with h disappear leaving;

which we commonly know, as the Power Rule. Crazy how that works huh? Moving along nicely
 The Bottom Line Definition of a Derivative (The Epsilon Delta Definition)
The Bottom Line Definition of a Derivative (The Epsilon Delta Definition)
So, after all the different ways we’ve been seeing to express a derivative, Mr. K Went on to talk about two things;
lowercase epsilon

and lowercase delta
 .
.
The official, Mr. K Definition of lowercase epsilon, is that epsilon is an infinitesimally small number. “Now how does this apply to graphs or derivatives?” you ask? It’s all quite simple. If you take a graph that you want to find a derivative of, and then pick a point, you would then proceed to move –epsilon units and +epsilon units from the x value of the point. After this you would end up with a small interval along the x-axis. This is the job of epsilon, to create this infinitesimally small interval. Then, what you would do, is move (from the –epsilon and +epsilon points) +delta and –delta from the y value of your original point. What you end up with, is essentially a super duper, ridiculously small “window” of the graph. Remember when we had the function, and all entered different viewing windows on our calculators? It’s the same effect here. Depending on what your “window” size is, the graph varies. In this instance, the epsilon delta window, forces every differentiable function, to look like a straight line. Thus, as a straight line, we may easily find the slope of the line, and therefore, the derivative of the graph. One thing to remember about this however is that epsilon is ALWAYS SMALL. However, delta may be very large, depending on the function. It is the infinitesimally small change in x which always results in the parent function being made into a straight line on that interval (if you remember, Mr. K said calculus is all about turning curves into lines. Here’s a perfect example!)
Okay, hopefully this image helps. The green dot represents the point. If you go back to the x axis you see + epsilon and - epsilon representing the interval part of the "window" is made from. Then if you go to the y axis, you see + and - delta representing the rest of the "window." When you take those intervals (+ and - epsilon, = and - delta) and follow them (the two red and blue lines here) you get a small window (the orange dotted line square.) inside this window, no matter what function (as long as its differentiable) you have, it will be turned straight. The fact that it only works inside the window is shown by the thinner purple line, that obviously, isn't straight ;p.
Graphing (sketching) the derivative graph of a parent function.
Okay, so after our huge almost entire class spanning detour from the main part of the lesson (that being the graph and drawing its first and second derivatives) we finally got down to this quick question.
Given the graph of f, sketch possible graphs for f’(x) and f’’(x)
So, since we know what the graph of f looks like, there’s a couple things we should do to sketch f’(x). First of all we need to find the critical points of the parent function. These are found wherever the parent function has a local minimum, or maximum. On the derivative graph of a function, a critical point (local min or max on parent function) ends up as a root of the derivative (the point lies on the x axis on the derivative.) Applying this to the graph we have here, we see that there are 2 critical points, and therefore, two roots. Lucky us!

Now that we’ve got our roots laid out, we’re going to look for our good old friend the inflection point. If you remember from the previous lessons, an inflection point, is where a graph changes concavity. This point relates to the derivative of the parent function in such a way that on the derivative graph, it becomes a local min or max.
 At this point, we have a pretty good framework of what our derivative graph should look like. The final thing to do, is look at the slopes of tangent lines drawn to the left and right, of the critical points on the parent graph (I believe this was called the first derivative test.) In this graph, a tangent line drawn to the left of the first critical point has a – slope, while one drawn the the right has a + slope. This suggests that the derivative graph, to the left of the critical point, is negative, and to the right of the critical point, is positive. The second critical point has a tangent line to the left with a + slope, and a tangent line with a – slope to the right. This suggests that on the derivative graph, to the left of the second critical point, the graph is +, while to the left of the critical point, it is -. In the image, the orange lines represent tangents taken from the left, and the magenta lines represent tangents taken from the right.
At this point, we have a pretty good framework of what our derivative graph should look like. The final thing to do, is look at the slopes of tangent lines drawn to the left and right, of the critical points on the parent graph (I believe this was called the first derivative test.) In this graph, a tangent line drawn to the left of the first critical point has a – slope, while one drawn the the right has a + slope. This suggests that the derivative graph, to the left of the critical point, is negative, and to the right of the critical point, is positive. The second critical point has a tangent line to the left with a + slope, and a tangent line with a – slope to the right. This suggests that on the derivative graph, to the left of the second critical point, the graph is +, while to the left of the critical point, it is -. In the image, the orange lines represent tangents taken from the left, and the magenta lines represent tangents taken from the right.
 Thus , with all this information, we can sketch a graph of f’(x). What we end up with is roughly, a parabola opening downwards. To find f’’(x) all you have to do, is follow the steps, treating f’(x) as the parent function. The first derivative is shown here in blue.
Thus , with all this information, we can sketch a graph of f’(x). What we end up with is roughly, a parabola opening downwards. To find f’’(x) all you have to do, is follow the steps, treating f’(x) as the parent function. The first derivative is shown here in blue.
 So to summarize, here’s the steps to sketching graphs of derivatives,
So to summarize, here’s the steps to sketching graphs of derivatives,
- Find the roots of f’(x). These are found at any local minimums or maximums on the parent function.
- Find the inflection points on the parent function (this turns into a local min or max on the first derivative graph.)
- Check the (signs) of slopes to the left and right of critical points (on the parent graph.) These give clues to the direction the derivative graph is travelling.
Repeating these steps, and you end up with the second derivative graph. The second derivative is shown here in magenta.
 Discontinuity and its flavors
Discontinuity and its flavors
Alrighty guys, here it is. The final topic of today’s lengthy discussions; discontinuity and it’s flavours.
Basically, according to Mr. K, there are 3 flavours, chocolate (Jump), Vanilla (Infinite) and Ripple (Removable). Let’s get to it.

Chocolate (Jump)

These are distinguished by, well… The huge jump in the middle of them.
Vanilla (Infinite)

These are distinguished by the fact that the graph hints at, gives clues to, insinuates, suggests, (or any other way you’d like to say, gives the general idea that) the graph goes to infinity, and that the only way to get from one part to the other, is to go to infinity, have lunch, and then come back. Definitely impossible, and thus, not entirely continuous.
Ripple (Removable)

These are probably the least life threatening of the three, as all that’s really going on with these is, somewhere, a point moves out of the way (is removed.) All you really need to do to make them continuous is put it back. My personal fav.
Conclusion
Okay. I think I’m finally done. After 3 days of piecing this thing together I can finally lay it to rest and officially, make Lawrence the final scribe of this cycle (says him.)
Before I do so I must first do the usual, and say that if anyone spots and discrepancies, or errors, you should tell me, so I can fix it mmkay? K. Also I was talking to Lawrence, and we were saying that there should be some way to veto being scribe. We were thinking you could have immunity challenges!
I can see it now,
“Jamie, you’ve won today's immunity challenge. You will be safe at tonight's scribal council.”
:D
(Note, this idea is not entirely serious, although it would be cool to see ;p)
Hopefully everyone is feeling better about the course, and less like these snowmen D:
Anyways That is all, I must go to bed now, and end this special edition of scribe posts! Remember, correct anything that's wrong (either via comment or w/e). Remember, Lawrence is the next scribe! :]











